Respuestas a la tarea 1

Respuestas

Pregunta 1

Considere el problema de regresión no lineal en el que la variable dependiente escalar \(y\) tiene una media condicional \(E(y_i)=g(x_i,\beta)\), siendo \(g(\cdot)\) una función no lineal. Suponga que:

El proceso generador de datos es \(y_i=g(x_i,\beta_0)+u_i\).
En el proceso generador de datos \(E(u_i|x_i)=0\) y \(E(uu'|X)=\Omega\), donde \(\Omega_{0,ij}=\sigma_{ij}\).
La función \(g(\cdot)\) satisface \(g(x, \beta^{(1)})=g(x, \beta^{(2)})\) si y solo si \(\beta^{(1)}=\beta^{(2)}\).
La matriz \(A_0\) existe y es finita y no singular y donde \(A_0=p\lim\frac{1}{N}\sum_{i=1}^{N}\left.\frac{\partial g_i}{\partial \beta}\right|_{\beta_0}\left.\frac{\partial g_i}{\partial \beta'}\right|_{\beta_0}=p\lim\frac{1}{N}\left.\frac{\partial g'}{\partial \beta}\frac{\partial g'}{\partial \beta'}\right|_{\beta_0}\)
\(N^{-1/2}\sum_{i=1}^N \left.\frac{\partial g_i}{\partial \beta}u_i \right|_{\beta_0}\xrightarrow{d}\mathcal{N}(0,B_0)\), donde \(B_0=p\lim \frac{1}{N}\sum_{i=1}^{N}\sum_{j=1}^{N}\sigma_{ij}\left.\frac{\partial g_i}{\partial \beta}\frac{\partial g_i}{\partial \beta'}\right|_{\beta_0}=p\lim\frac{1}{N}\left.\frac{\partial g'}{\partial \beta}\Omega_0 \frac{\partial g}{\partial \beta'}\right|_{\beta_0}\).

Respuestas: ver proposición 5.6 en CT.

[5 puntos] Plantee el problema de optimización para la minimización de la suma de los errores cuadráticos y obtenga las condiciones de primer orden.
[10 puntos] Pruebe que \(\hat{\beta}_{MCNL}\), el estimador de mínimos cuadrados no lineales (MCNL) y definido como una raíz de las condiciones de primer orden, es consistente para \(\beta_0\).
[10 puntos] Derive una expresión para \(\sqrt{N}(\hat{\beta}_{MCNL}-\beta_0)\) y pruebe que \(\sqrt{N}(\hat{\beta}_{MCNL}-\beta_0)\xrightarrow{d}\mathcal{N}(0,A_0^{-1}B_0A_0^{-1})\). Tip: utilice una expansión de Taylor exacta de primer orden.
[5 puntos] ¿Cómo estimaría \(V(\hat{\beta}_{MCNL})\)?}

Pregunta 2

Suponga que está interesado en una variable aleatoria que tiene una distribución Bernoulli con parámetro \(p\). La función de densidad está definida como:

\[f(x_;p)=\left\{\begin{array} .1 & \text{con probabilidad } p \\ 0 & \text{con probabilidad } 1-p \end{array} \right.\] Suponga que tiene una muestra de \(N\) observaciones independientes e idénticamente distribuidas.

[4 puntos] Plantee la función de log verosimilitud del problema.

Podemos escribir la función de densidad para la \(i\)-ésima observación como

\[f(x_i;p)=p^{x_i}(1-p)^{(1-x_i)}\]

Por tanto, la función de verosimilitud es

\[L_N(p)=\prod_{i=1}^N f(x;p)=\prod_{i=1}^N p^{x_i}(1-p)^{(1-x_i)} = p^{\sum_{i=1}^N x_i}(1-p)^{N-\sum_{i=1}^N x_i}\]

Y la función de log verosimilitud será

\[\mathcal{L_N(p)}=\ln{L_N(p)}=\sum x_i \ln(p)-(N-\sum x_i)\ln(1-p)\]
[4 puntos] Obtenga las condiciones de primer orden y resuelva para \(\hat{p}\).

Derivando \(\mathcal{L}_N\) con respecto a \(p\) obtenemos la condición de primer orden:

\[\frac{d\mathcal{L}_N(p)}{d p}=\frac{\sum x_i}{p}-\frac{N-\sum x_i}{1-p}=0\]

Y resolviendo, obtenemos el estimador de máxima verosimilitud \[\hat{p}_{MV}=\bar{x}\] es decir, la media muestral.
[2 puntos] ¿Cuál es la media y la varianza del estimador de máxima verosimilitud que ha encontrado?

Obtenemos directamente la media \[E(\hat{p}_{MV})=E(\bar{x})=\frac{1}{N}E\left(\sum x_i\right)=\frac{1}{N}N p=p\]

Mientras que la varianza es \[V(\hat{p}_{MV})=\frac{1}{N^2}V\left(\sum x_i\right)=\frac{p(1-p)}{N}\]

Pregunta 3

Considere el modelo logit:

\[f(y_i|x_i;\theta_0)=\left\{ \begin{array} .1 & \frac{\exp\{x_i'\theta_0\}}{1+\exp\{x_i'\theta_0\}} \\ 0 & \frac{1}{1+\exp\{x_i'\theta_0\}} \end{array} \right.\] donde \(x_i\) es un vector de variables explicativas, \(\theta_0\) y es el vector de parámetros poblacional. Asuma que dispone de observaciones \((y_i,x_i)\) que son iid.

[5 puntos] Escriba la función de log verosimilitud condicional para la observación \(i\).

Es conveniente escribir el problema en término de \(\Lambda (x_i'\theta_0) \equiv \frac{\exp\{x_i'\theta_0\}}{1+\exp\{x_i'\theta_0\}}\). Así, la función de verosimilitud para la observación \(i\) es:

\[f(y_i|x_i;\theta_0)=\Lambda (x_i'\theta_0)^{y_i}(1-\Lambda (x_i'\theta_0))^{(1-y_i)}\]

Tomando logs, la función de log verosimilitud es:

\[\mathcal{l}(y_i|x_i,\theta)=\ln f(y_i|x_i;\theta)=y_i\ln \Lambda (x_i'\theta)+(1-y_i)(1-\Lambda (x_i'\theta))\]
[5 puntos] Encuentre el vector score para la observación \(i\).

El vector score es el vector de primeras derivadas parciales de la log verosimilitud. Un pequeño truco facilita las cosas. Se puede mostrar que \(\Lambda (\cdot)'=\Lambda (\cdot)(1-\Lambda (\cdot))\). Entonces:

\[\frac{\partial \mathcal{l}_i}{\partial\theta}=y_i \frac{1}{\Lambda (x_i'\theta)}\Lambda (x_i'\theta)(1-\Lambda (x_i'\theta))x_i+(1-y_i)\frac{1}{1-\Lambda (x_i'\theta)}\Lambda (x_i'\theta)(1-\Lambda (x_i'\theta))x_i\]

Simplificando:

\[\frac{\partial \mathcal{l}_i}{\partial\theta}=(y_i-\Lambda (x_i'\theta))x_i \equiv s(y_i,x_i;\theta)\]
[5 puntos] Encuentre la hesiana de la función de log verosimilitud con respecto a \(\mathbf{\theta}\).

Procedemos a derivar el score con respecto a \(\theta'\):

\[H(y_i,x_i;\theta)\equiv \frac{\partial s(y_i,x_i;\theta)}{\partial \theta'}= -\Lambda(x_i'\theta)(1-\Lambda(x_i'\theta))x_ix_i'\]
[5 puntos] Obtenga la matriz de información para la observación \(i\).

La matriz de información es \(E(s(y_i,x_i;\theta_0)s(y_i,x_i;\theta_0)'|x_i)\)

\[I(\theta_0)=E((y_i-\Lambda(x_i'\theta_0))^2x_ix_i')\]

Pregunta 4

Suponga una variable aleatoria \(X_i\) con distribución desconocida. Sin embargo, sí conocemos que \(E(X)=\mu=54\) y que \(\sqrt{V(X)}=\sigma=6\). Suponga que se recolecta una muestra de 50 observaciones.

[2 punto] ¿Cuál es la distribución asintótica de la media muestral \(\bar{X}\)?

Si se puede aplicar un teorema de límite central a la media muestral, sabemos que la nueva variable hereda la media de \(X_i\) y la desviación estándar es la desviación estándar de \(X_i\) dividida por la raíz del tamaño de la muestra. Es decir:

\[\bar{X}\sim \mathcal{N}(54, 6^2/50)\]
[4 punto] ¿Cuál es la probabilidad de que \(\bar{X}>58\)?

Sabemos que \(\frac{\bar{X}-54}{6/\sqrt{50}}\sim\mathcal{N}(0,1)\), por tanto:

\[P(\bar{X}>58)=P\left(z>\frac{58-54}{6/\sqrt{50}}\right)=P(z>4.714045)=1-\Phi(4.714045)\]

Calculamos la probabilidad usando pnorm, que nos da la función de distribución. La probabilidad es un número muy pequeño:
```
1-pnorm((58-54)/(6/sqrt(50)), mean = 0, sd = 1)
```
```
[1] 1.214234e-06
```
[2 punto] ¿Cuál es la probabilidad de que una observación elegida al azar sea tal que \(X_i>58\)?

Es imposible de determinar porque no sabemos la distribución de \(X_i\). Esto es algo muy conveniente de los TLC, pues nos permiten hacer afirmaciones sobre la media muestral sin saber la distribución de la que provienen las observaciones. Solo necesitamos que se cumplan las condiciones sobre las \(X_i\) para aplicar los TLC.
[2 punto] Provea un intervalo de confianza de 99% para la media muestral.

Por un lado, sabemos que la variable aleatoria \(Z=\frac{\bar{X}-\mu}{\sigma/\sqrt{N}}\) tendrá una distribución \(\mathcal{N}(0,1)\). Por otro lado, queremos obtener \(P(-z_{\alpha/2}<Z<z_{\alpha/2})=0.99\). Manipulando, obtenemos una expresión para el intervalo de confianza:

\[\left(\bar{X}-z_{\alpha/2}\frac{\sigma}{\sqrt{N}},\bar{X}+z_{\alpha/2}\frac{\sigma}{\sqrt{N}}\right)\]

En nuestro caso, el intervalo es:

\[P\left(\bar{X}\pm 2.5758\times(6/\sqrt{50})\right)=0.99\]

donde obtenemos el 2.5758 como:
```
qnorm(0.995)
```
```
[1] 2.575829
```
qnorm es la función cuantil y está definida como la función inversa de la función de distribución. La función cuantil da el valor de \(x\) tal que \(F(x)=P(X \leq x)=p\).

Entonces, el intervalo de confianza es: \[P(\bar{X}\pm 2.185664)=0.99\]

Pregunta 5

En esta pregunta mostraremos los alcances de los teoremas del límite central. Para esto, generaremos muchas muestras de tamaño \(N\) con una distribución \(Bernoulli\) con probabilidad de éxito \(p=0.7\). Recuerde que cuando realice simulaciones, siempre debe fijar una semilla al inicio para poder replicar su trabajo.

[2 puntos] ¿Cuál es la media y la varianza de una variable aleatoria \(y_i \sim Bernoulli(0.3)\)?

Para una variable que se distribuye \(Bernoulli(p)\), la media es \(p\) y la varianza es \(p(1-p)\). Para este caso, \(E(y_i)=0.7\) y \(V(y_i)=0.7*0.3=0.21\).
[2 puntos] Si \(y_i\) son iid y podemos aplicar un teorema de límite central, ¿cuál es la distribución teórica de \(\bar{y}\) cuando \(N\to\infty\)?

Obtenemos el valor esperado y la varianza de \(\bar{y}\):

\[E(\bar{y})=\frac{1}{N}E(\sum_i y_i) = E(y_i)=p\]

\[V(\bar{y})=\frac{1}{N^2}V(\sum_i y_i) = \frac{1}{N}V(y_i)=\frac{p(1-p)}{N}\]

Entonces, un TLC nos daría las condiciones para que:

\[\frac{\bar{y}-0.7}{\sqrt{0.21/N}}\sim\mathcal{N}(0, 1)\]
[5 puntos] Realice el siguiente procedimiento \(J=1,000\) veces. Obtenga una muestra de tamaño \(N=3\) a partir de la distribución \(Bernoulli(0.7)\) y calcule la media muestral \(\bar{y}\). Coleccione las \(J\) medias muestrales y luego grafique un histograma de las medias muestrales obtenidas junto con una curva teórica normal con la media y varianza obtenida en la parte b. Comente sobre lo que observa.
```
set.seed(921)
reps <- 1000
n <- 3
p <- 0.7
v <- p*(1-p)/n

ymedias3 <- numeric(reps)
for (i in 1:reps){
 sample <- rbinom(n, 1, p)
 ymedias3[i]<-mean(sample)
}
```
Graficamos junto con una densidad \(N(0.7, \sqrt{0.21/3})\):
```
hist(ymedias3, breaks=20, prob=TRUE, 
     xlab="Medias")
curve(dnorm(x, mean=p, sd=sqrt(v)), 
      col="darkblue", lwd=2, add=TRUE, yaxt="n")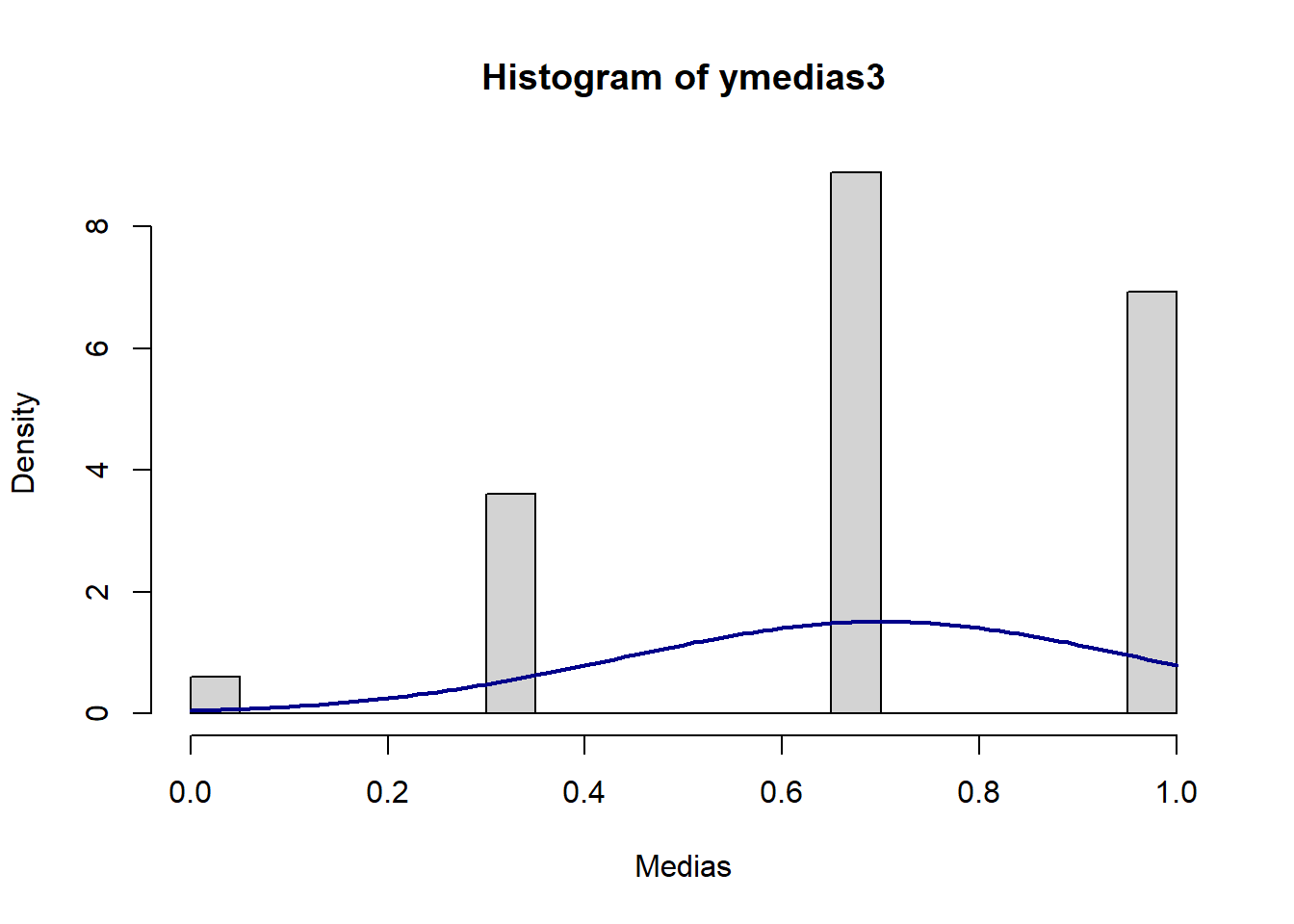
```
El histograma no se parece nada a la curva normal.

[3 puntos] Repita lo realizado en la parte b., ahora con \(N=15\). Comente sobre lo que observa.

reps <- 1000
n <- 15
p <- 0.7
v <- p*(1-p)/n

ymedias15 <- numeric(reps)
for (i in 1:reps){
 sample <- rbinom(n, 1, p)
 ymedias15[i]<-mean(sample)
}

Graficamos junto con una densidad \(N(0.7, \sqrtt{0.21/15})\):

hist(ymedias15, breaks=20, prob=TRUE)
curve(dnorm(x, mean=p, sd=sqrt(v)), 
      col="darkblue", lwd=2, add=TRUE, yaxt="n")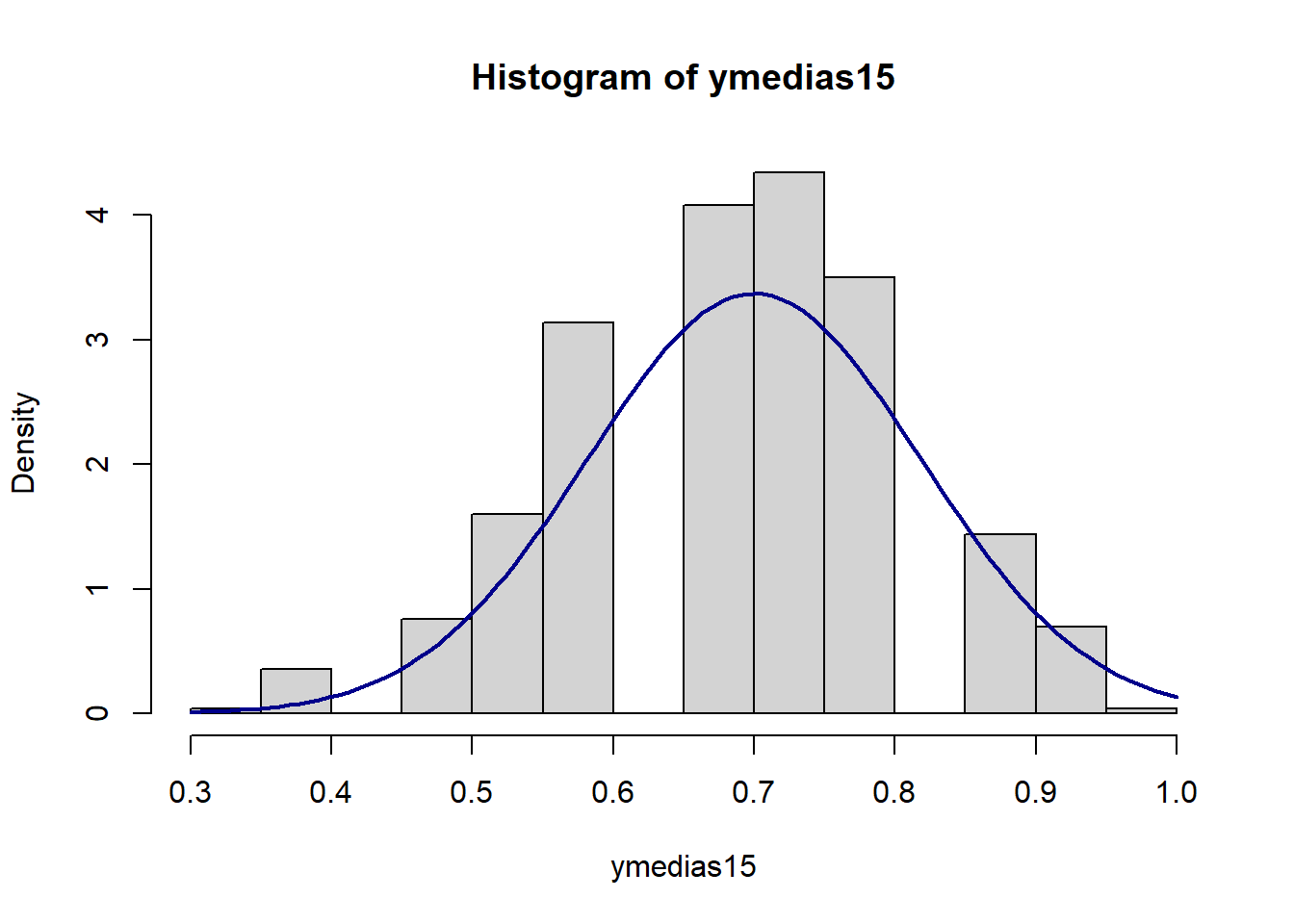

El histograma comienza a tener una forma normal.

[3 puntos] Repita lo realizado en la parte b., ahora con \(N=1,500\). Comente sobre lo que observa.

#|echo: true

reps <- 1000
n <- 1500
p <- 0.7
v <- p*(1-p)/n

ymedias1500 <- numeric(reps)
for (i in 1:reps){
 sample <- rbinom(n, 1, p)
 ymedias1500[i]<-mean(sample)
}

Graficamos junto con una densidad \(N(0.7, \sqrt{0.21/1500})\):

hist(ymedias1500, breaks=20, prob=TRUE, 
     xlab="Medias")
curve(dnorm(x, mean=p, sd=sqrt(v)), 
      col="darkblue", lwd=2, add=TRUE, yaxt="n")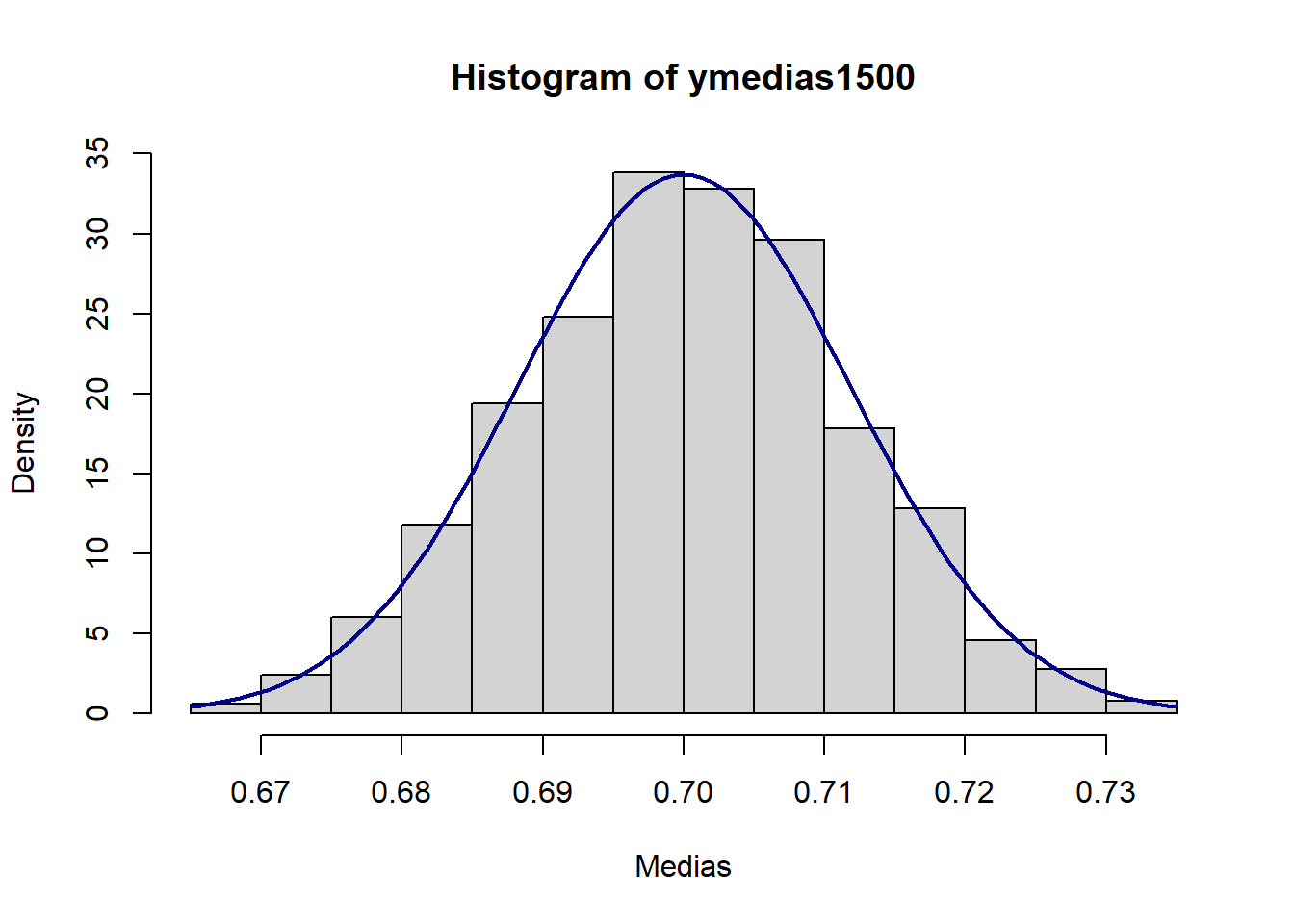

El histograma se parece ya a la curva normal. Podrían repetir este ejercicio con un tamaño de muestra más grande incluso y ver qué sucede.

[5 puntos] ¿Cómo usaría este ejercicio con palabras simples para explicar a una persona que no sabe mucho de estadística sobre la importancia de los teoremas de límite central?

Un TLC nos permite hacer afirmaciones sobre la distribución de un estadístico. Un estadístico es un resumen de los datos, por lo que nos interesa usar dichos estadísticos para describir características de los fenómenos que estudiamos usando datos. Queremos saber cosas como lo que esperamos en promedio que suceda con una variable, o qué tanta variabilidad dicha variable tendrá en la población. Con un TLC podemos hacer afirmaciones sobre cómo lucen promedios muestrales de la variable que estudiamos cuando tenemos suficientes observaciones. Nos dice en particular que va a tener una distribución normal.

Pregunta 6

Sea \(x_1\) un vector de variables continuas, \(x_2\) una variable continua y \(d_1\) una variable dicotómica. Considere el siguiente modelo probit: \[P(y=1│x_1,x_2 )=\Phi(x_1'\alpha+\beta x_2+\gamma x_2^2 )\]

[5 punto] Provea una expresión para el efecto marginal de \(x_2\) en la probabilidad. ¿Cómo estimaría este efecto marginal?

El efecto marginal de interés es:

\[\frac{\partial P(y=1|x_1,x_2)}{\partial x_2}=\phi(x_1\alpha+\beta x_2+\gamma x_2^2)(\beta+2\gamma x_2)\]

Para estimarlo, usamos máxima verosimilitud para obtener estimadores consistentes de \(\alpha\), \(\beta\) y \(\gamma\) y empleamos software para obener los valores de las probabilidad usando las características individuales \(x_1\) y \(x_2\). Luego podemos obtener el efecto marginal promedio como el promedio de los efectos marginales individuales. Alternativamente, se podría calcular el efecto marginal en valores específicos de \(x_1\) y \(x_2\), como \(\bar{x}_1\) y \(\bar{x}_2\).
[3 punto] Considere ahora el modelo: \[P(y=1│x_1 ,x_2 ,d_1)=\Phi(x_1 '\delta+\pi x_2+\rho d_1+\nu x_2 d_1 )\] Provea la nueva expresión para el efecto marginal de \(x_2\).

El efecto marginal es: \[\frac{\partial P(y=1|x_1,x_2)}{\partial x_2}=\phi(x_1\delta+\pi x_2+\rho d_1+ \nu x_2d_1)(\pi+\nu d_1)\]
[2 punto] En el modelo de la parte b., ¿cómo evaluaría el efecto de un cambio en \(d_1\) en la probabilidad? Provea una expresión para este efecto.

Dado que \(d_1\) es una variable dicotómica, el efecto de \(d_1\) se mide como la diferencia en probabilidad cuando \(d_1=1\) y cuando \(d_1=0\):

\[P(y=1|x_1,x_2,d_1=1)-P(y=1|x_1,x_2,d_1=0)=\phi(x_1\delta+(\pi+\nu)x_2+\rho)-\phi(x_1\delta+\pi x_2)\]

Podemos estimar este cambio en probabilidad para cada individuo de la muestra y luego obtener un promedio de los cambios en probabilidad. Por ejemplo, supongamos que estudiamos la probabilidad de estar empleado y que \(d_1\) es la pertenencia o no a un sindicato. Para cada individuo en la muestra obtemeos el cambio en probabilidad que resulta de que \(d_1\) pase de 1 a 0.