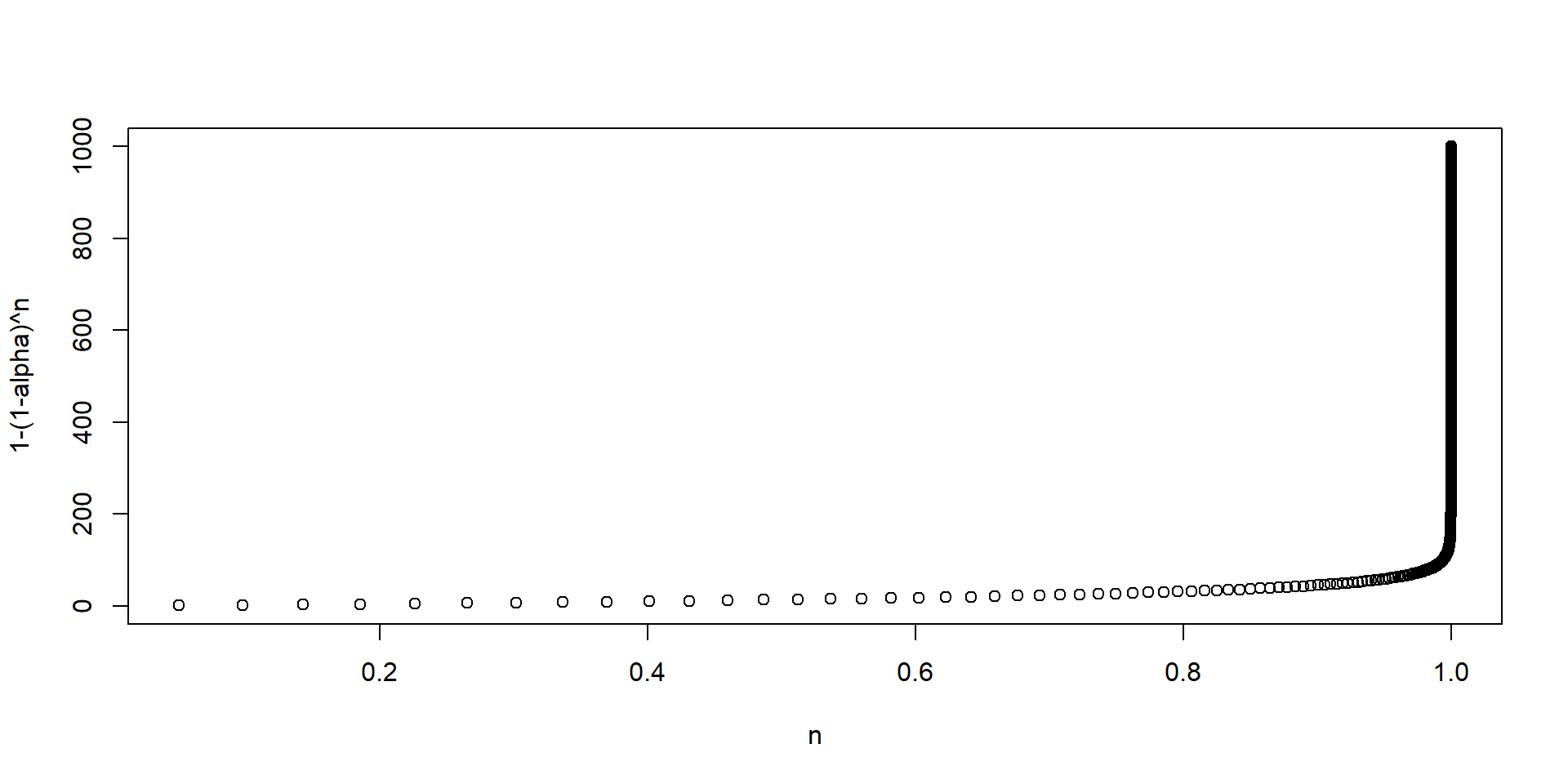Hipótesis múltiples
Inferencia Causal
Irvin Rojas
rojasirvin.com
Centro de Investigación y Docencia Económicas División de Economía
Hipótesis múltiples
Hipótesis múltiples
Error tipo I: concluir que hay un efecto de tratamiento cuando la \(H_0\) es verdadera, es decir, cuando \(H_0:\;\beta_i=0\)
En una investigación fijamos \(\alpha\), la probabilidad de rechazar \(H_0\) cuando \(H_0\) es cierto
En economía trabajamos con \(\alpha=0.05\) o \(\alpha=0.01\)
El problema con probar múltiples hipótesis es que inflamos la tasa de error tipo I
- Por ejemplo, si tenemos 100 hipótesis y si usamos un valor estándar de \(\alpha=0.05\), esperaríamos rechazar 5 hipótesis por suerte
Hipótesis múltiples
Si realizamos una prueba, la probabilidad de cometer un error es \(\alpha\) y la de no cometer un error es \(1-\alpha\)
Si realizamos \(n\) pruebas, la probabilidad de no cometer un error es \((1-\alpha)^n\) y la probabilidad de cometer al menos un error es \(1-(1-\alpha)^n\)
Es decir, la probabilidad de cometer al menos un error se incrementa exponencialmente
Hipótesis múltiples
- Dos estrategias que abordaremos son:
- Controlar o ajustar \(\alpha\)
- Crear índices que agreguen varias variables
Control del error tipo I
Control del error tipo I
- Popper (1995), Multiple Hypothesis Testing
- Definimos familias de variables
- Haremos el ajuste hacia adentro de estas familias
- Antes habíamos estudiado de Banerjee et al. (2015)
- Seguridad alimentaria
- Consumo
- Activos
- Salud mental
- Dentro de cada familia tenemos \(n\) hipótesis \(H_i\), con un valor \(p\) asociado \(p_i\)
- Recordemos que \(p_i\) es la probabilidad de que el estadístico \(T_i\) exceda el valor teórico \(t_i\)
- Ordenamos las hipótesis de menor a mayor,con \(p_1\) siendo el valor más pequeño: \(p_1\leq p_2\ldots \leq p_n\)
Método de Bonferroni
- El método propuesto por Bonferroni controla la tasa de error por familia (FEWR por family-wise error rate) definida como la probabilidad de cometer al menos un error tipo I
Consiste en rechazar \(H_i\) si \(p_i\leq \alpha_i\), donde \(\alpha_i\) se escoge de forma que \(\sum_i\alpha_i=\alpha\)
Usualmente se hace \(\alpha_i=\frac{\alpha}{n}\)
- Por ejemplo, con dos tests y \(\alpha=0.05\), \(\alpha_i^B=0.025\)
- Noten que esta corrección es bastante conservadora
- También podemos ver este test como crear unos valores \(p^B\) ajustados: \(p_i^B=p_i\times n\)
¿Por qué preocuparnos por la FWER?
La idea de la FWER tiene sentido si nos preocupa tener incluso un solo falso positivo
En la práctica, podemos vivir con algunos falsos positivos
Método de Benjamini y Hochberg
Este método controla la tasa de falso descubrimiento
Si \(V\) es el número de falsos rechazos (cuando rechazamos la \(H_0\) que es verdadera) y si \(R\) es el número total de rechazos, entonces \(Q=V/R\) es la proporción de falsos rechazos
Al valor esperado de \(Q\) se le conoce como tasa de falsos rechazos (FDR por false discovery rate)
Sea \(k\) el más grande de los \(i\) tal que \[p_i\leq\frac{i}{n}\alpha\] entonces rechazar todos los \(H_i\) para \(i=1,2,\ldots,k\)
En la práctica usamos R
Ejemplo: Benjamini & Hochberg (1995)
Ejemplo: Bonferroni
# A tibble: 15 × 4
poriginal hipotesis bonferroni_alpha bonferrini_rechazar
<dbl> <dbl> <dbl> <dbl>
1 0.0001 1 0.00333 1
2 0.0004 2 0.00333 1
3 0.0019 3 0.00333 1
4 0.0095 4 0.00333 0
5 0.0201 5 0.00333 0
6 0.0278 6 0.00333 0
7 0.0298 7 0.00333 0
8 0.0344 8 0.00333 0
9 0.0459 9 0.00333 0
10 0.324 10 0.00333 0
11 0.426 11 0.00333 0
12 0.572 12 0.00333 0
13 0.653 13 0.00333 0
14 0.759 14 0.00333 0
15 1 15 0.00333 0Ejemplo: Benjamini & Hochberg
# A tibble: 15 × 4
poriginal hipotesis bh_alpha bh_rechazar
<dbl> <dbl> <dbl> <dbl>
1 0.0001 1 0.00333 1
2 0.0004 2 0.00667 1
3 0.0019 3 0.01 1
4 0.0095 4 0.0133 1
5 0.0201 5 0.0167 0
6 0.0278 6 0.02 0
7 0.0298 7 0.0233 0
8 0.0344 8 0.0267 0
9 0.0459 9 0.03 0
10 0.324 10 0.0333 0
11 0.426 11 0.0367 0
12 0.572 12 0.04 0
13 0.653 13 0.0433 0
14 0.759 14 0.0467 0
15 1 15 0.05 0Índices
Creación de \(z\)-scores
Otra forma comúnmente usada de evitar el problema de las múltiples hipótesis es crear índices
Kling, Liebmand y Katz (2007) proponen el siguiente promedio de los \(z\)-score para generar un solo índice
Definir las familias y las variables que componen cada familia, donde \(y_{ij}\) es la \(j\)ésima variable en la familia con \(J\) variables
Definir las variables \(y_{ij}\) de tal forma que mayores valores se interpreten como mejora
Crear \(z_{ij}\) como \(z_{ij}=\frac{y_{ij}-\bar{y_j}^C}{sd(y_j)^C}\sim(0,1)\), es decir, estandarizar cada una de las \(J\) variables usando al grupo de control como referencia
Crear \(z_i\), un solo índice para cada individuo que agregue los \(J\) índices creados antes
El procedimiento descrito en Banerjee et al. (2015) es bastante general, pues incluye el caso donde hay varias rondas de seguimiento y varios países
Creación de \(z\)-scores
Podemos escribir el índice descrito como
\[z_i=\frac{(\frac{1}{J}\sum_j z_{ij})-\bar{z}_j^C}{sd(z_j^C)}\]
Esta transformación tiene la ventaja de que en la siguiente regresión de efecto de tratamiento
\[z_i=\alpha+\beta T_i + X_i'\gamma+\varepsilon_i\]
el coeficiente \(\beta\) se interpreta como el efecto del tratamiento medido en desviaciones estándar con respecto a la media del grupo de control
Noten que todos las variables dentro de la familia pesan igual
Quizás nos gustaría tomar en cuenta la correlación entre las variables dentro del índice
Índice de Anderson
- Anderson (2008) propone el siguiente índice, que puede verse como una generalización del de Kling:
\[\bar{s}_i=\frac{1}{W_{i}}\sum_{j\in J} w_j z_{ij}\]
\(w_j\) es el peso para la variable \(j\) y \(W_i=\sum_{j\in J}w_{j}\)
Los pesos son una función de la matriz de covarianzas entre las variables que conforman la familia
Material de clase en versión preliminar.
No reproducir, no distribuir, no citar.