Regresión y efectos causales
Inferencia Causal
Irvin Rojas
rojasirvin.com
Centro de Investigación y Docencia Económicas División de Economía
Motivación del uso de regresión en evaluación
Regresión como función de esperanza condicional
Olvidemos por ahora la causalidad y centremonos en la conexión entre dos variables, \(y\) y \(s\) (ingreso y educación)
La función de esperanza condicional es una forma de describir la relación entre estas dos variables
Función de esperanza condicional: la FEC de \(y_i\) dado un vector de regresores \(X_i\) es la esperanza o promedio poblacional de \(y_i\) cuando mantenemos fijo \(X_i\) y se denota \(E(y_i|X_i)\)
Para representar una realización particular de \(X_i\) escribimos \(X_i=x_i\), por lo que la FEC es \(E(y_i|X_i=x_i)\)
Con \(y_i\) discreta, la FEC se expresa como
\[E(y_i|X_i=x_i)=\sum_t t P(y_i=t|X_i=x_i)\]
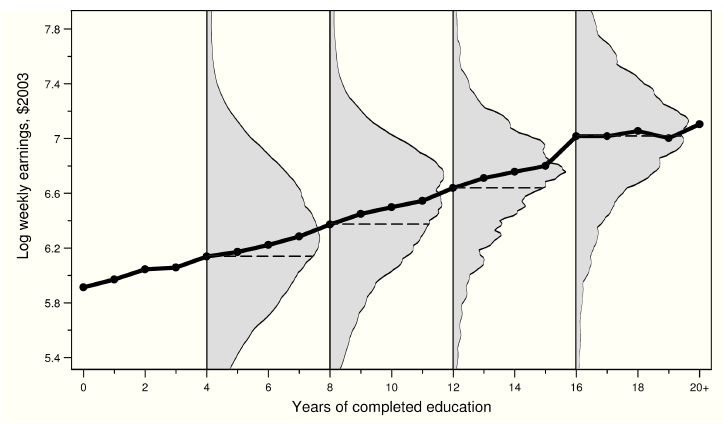
Ejemplo de FEC: salarios y educación en Estados Unidos
- La figura 3.3.1 en MHE muestra la FEC de salarios en Estados Unidos
- Para cada año de educación, vemos cuál es el (log) del ingreso semanal
- La figura muestra dos cosas principales:
- La clara relación positiva entre salarios y educación
- La gran variabilidad en salarios para un nivel de educación dado
Teorema de la regresión de la FEC
- MHE provee varias motivaciones de usar regresión al relacionar la función de regresión con la FEC
- Aquí vamos a rescatar el que considero más intuitivo
- Teorema de la regresión de la FEC: la función \(X_i'\beta\) es la aproximación lineal de mínimos errores cuadrados promedio de \(E(y_i|X_i)\):
\[\beta=\arg\min_b E((E(y_i|X_i)-X_i'b) ^2)\]
- Lo que nos dice este teorema es que si yo quiero aproximar la FEC y mi criterio para obtener la mejor aproximación es un problema de mínimos cuadrados promedio, entonces lo mejor que puedo hacer es que mi aproximación sea \(X'\beta\)
Teorema de la regresión de la FEC
- Este teorema nos dice que si pensamos en en aproximar \(E(y_i|X_i)\), incluso aunque la FEC no sea lineal, la función de regresión nos da la mejor aproximación lineal
- Este teorema es lo más cercano a como interpretamos la regresión en evaluación pues más que querer predicciones de \(y\) para un individuo \(i\), nos interesa la relación promedio entre las variables
- Vale la pena notar que aquí hablamos de la función de regresión poblacional, es decir, aún tenemos que hablar sobre cómo estimarla
Teorema de la regresión de la FEC
Demostración: para la demostración, consideren el problema de regresión poblacional: \[\beta=\arg\min_b E((y_i-X_i'b)^2)\]
Podemos sumar y restar \(E(y_i|X_i)\) y reescribir \((y_i-X_i'b)^2\) como:
\[(y_i-X_i'b)^2 = ((y_i-E(y_i|X_i))+(E(y_i|X_i)+X_i'b))^2= \\ =(y_i-E(y_i|X_i))^2+(E(y_i|X_i)-X_i'b)^2+2(y_i-E(y_i|X_i))(E(y_i|X_i)-X_i'b)\]
El término \((y_i-E(y_i|X_i))^2\) no involucra \(b\) por lo que no importa en el proceso de optimización
Por la Propiedad de Descomposición de la FEC, \(2(y_i-E(y_i|X_i))(E(y_i|X_i-X_i'b))=0\)
Nos queda \((E(y_i|X_i)+X_i'b)^2\), que es exactamente el mismo problema que el del Teorema de la regresión de la FEC
Teorema de la regresión de la FEC
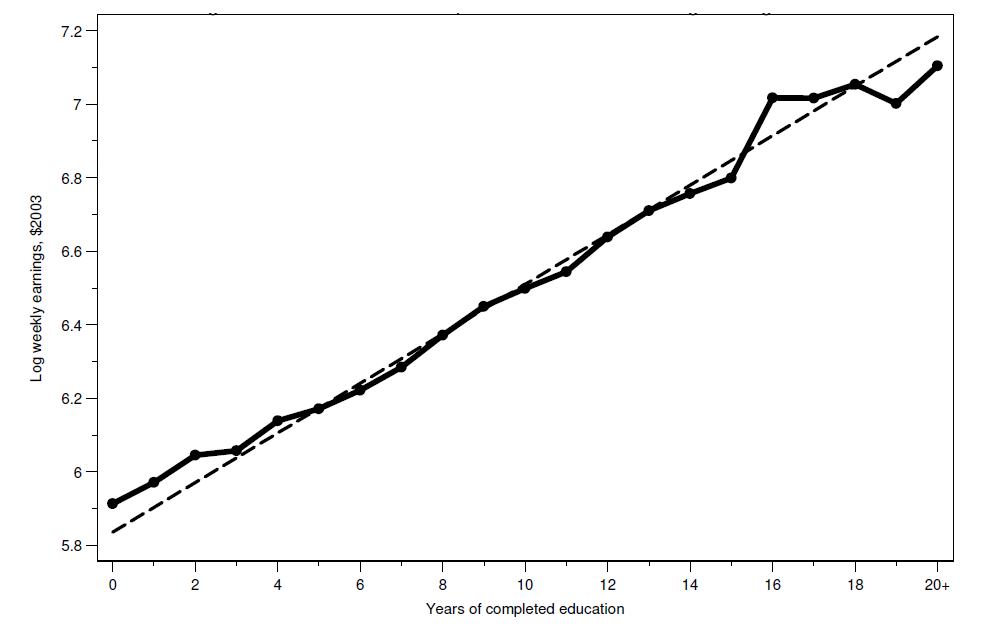
- La figura 3.1.2 en MHE ilustra este teorema
- La línea sólida es la FEC de la relación años de educación - salario
- La línea sólida muestra los promedios del salario para cada año de educación
- La línea quebrada muestra la línea de regresión usando microdatos
- Graficar el coeficiente \(\beta\) que resulta al correr \(y_i=\alpha+\beta s_i+u_i\)
- El teorema de la regresión de la FEC dice que obtenemos la misma recta si hacemos una regresión de \(E(y_i|s_i)=\alpha+\beta s +u\)
- Es decir, calculamos las medias del salario para cada nivel de educación y luego se hacemos una regresión de las medias en función de los niveles de educación (dándole más peso a las observaciones que aportaron más datos a la media de cada nivel)
Modelos saturados
Son modelos de regresión donde incluimos una variable categórica para cada uno de los posibles valores que tomen las \(X_i\)
Del ejemplo con los datos de EUA, hay 21 posibles años de educación, entonces un modelo saturado es:
\[y_i=\alpha+\beta_1 c_{1i} + \beta_2 c_{2i} + \ldots + \beta_{21} c_{21i} + u_i\] donde \(c_{ji}=1\) si el individuo \(i\) tiene una educación \(s_{i}=j\)
- El \(j\)-ésimo coeficiente \(\beta_j\) es el efecto de tener el nivel de educación \(j\)
- Además, \(\alpha=E(y_i|s_i=0)\), se conoce como la categoría omitida
- Podemos escoger la categoría omitida que tenga más sentido
Modelos saturados
- Si tuviéramos dos características, sexo y urbano-rural, un modelo saturado incluye un término interacción:
\[y_i=\alpha+\beta_H x_{Hi} + \beta_R x_{Ri}+ \beta_{HR} x_{Hi}x_{Ri}+u_i\]
A los coeficientes \(\beta_H\) y \(\beta_U\) se les conoce como efectos principales
El término de interacción \(\beta_{HR}\) nos dice cómo cambia el ingreso entre individuos por tipo de localidad y por sexo
- Un modelo saturado, si usamos sexo y \(\tau\) categorías de educación, sería: \[y_i=\alpha+\beta_H x_{Hi}+\sum_{j=1}^{\tau} \beta_j c_{ji} + \sum_{j=1}^{\tau}\beta_{Hj}(x_{Hi}c_{ji}) + u_i\]
Regresión y causalidad
Regresión y causalidad
Lo que hemos visto hasta ahora nos dice que la regresión es nuestro mejor aproximación lineal a la FEC
Pero la regresión será causal solo si la FEC es causal
Con lo que hemos visto del modelo de resultados potenciales, podemos tener una interpretación causal de la FEC
- La FEC es causal cuando describe las diferencias en resultados potenciales promedio para una población de referencia fija (Angrist and Pischke, 2009)
- En la relación entre educación y salarios, una FEC causal describiría lo que un individuo ganaría con distintos niveles de educación
- Hay otro caso en el que la regresión puede tener interpretación causal, cuando existe selección basada en observables
Supuesto de independencia condicional
- El supuesto de independencia condicional significa que, condicional en una serie de características \(X_i\), el sesgo de selección desaparece:
\[\{y_{0i},y_{1i}\}\perp D_i | X_i\]
- Supongamos que \(D_i\) es ir o no a la universidad y la variable de interés es el ingreso
- Sabemos que la comparación observacional nos da:
\[ \begin{aligned} E(y_i|D_i=1)-E(y_i|D_i=0)=&\overbrace{ E(y_{1i}-y_{0i}|D_i=1)}^{\text{Efecto promedio en los tratados}}+\\& \underbrace{E(y_{0i}|D_i=1)-E(y_{oi}|D_i=0)}_{\text{Sesgo de selección}} \end{aligned} \]
- Es posible que aquellos que no fueron a la universidad de todos modos hubieran tenido un mayor salario, por lo que el sesgo de selección es positivo
Supuesto de independencia condicional
El SIC implica que si hacemos la comparación condicional en \(X_i\), el sesgo desaparece \[ \begin{aligned} E(y_i|X_i,D_i=1)-E(y_i|X_i,D_i=0)=E(y_{1i}-y_{0i}|X_i) \end{aligned} \]
Es decir, que si comparamos a personas con y sin tratamiento, con los \(X_i\) fijos, el sesgo de selección desaparece
Mantener fijas las \(X\) es el análogo a obtener el promedio del salario en cada nivel de escolaridad en la gráfica de la FEC descrita anteriormente
Supuesto de independencia condicional
Para generalizar el concepto cuando la variable tiene más de dos valores (como con la educación \(s_i\)), escribamos \(Y_{si}\equiv f_i(s)\)
Esta función nos dice cuál sería el ingreso de \(i\) bajo todos los posibles niveles de \(s\)
En este caso, asumimos el SIC, que se traduce en: \[Y_{si}\perp s_i | X_i\]
En diseños experimentales, el SIC surge porque el tratamiento se asigna de forma aleatoria
Pero con datos observacionales, el SIC significa que \(s_i\) es casi como si fuera asignado de manera aleatoria cuando condicionamos en \(X_i\)
Supuesto de independencia condicional
- En los datos solo observamos \(Y_i=f_i(s_i)\)
- Dado el SIC, podemos hacer comparaciones de ingreso promedio para distintos niveles de educación: \[E(Y_i|X_i,s_i=s)-E(Y_i|X_i,s_i=s-1)=E(f_i(s)-f_i(s-1)|X_i)\]
- Notemos que lo impráctico de esto es que tendríamos que hacer comparaciones en pares y luego tratar de hacer un promedio ponderado por el número de individuos en cada nivel de educación
Regresión para hacer las comparasiones
- Supongamos una función causal para el ingreso \[f_i(s)=\alpha+\rho s+\nu_i\]
que indica lo que un individuo ganaría para todo valor de \(s\) (y no solo el valor realizado \(s_i\))
La única parte aleatoria es el error con media cero \(\nu_i\), que captura los factores no observados que afectan los ingresos
Sustituyendo el valor observado:
\[Y_i=\alpha+\rho s_i+\nu_i\]
- \(s_i\) puede estar correlacionado con los resultados potenciales \(f_i(s)\), es decir, correlacionado con el error \(\nu_i\)
Regresión para hacer las comparasiones
Supongamos que el SIC se cumple dado un vector \(X_i\)
Descompongamos el error en una función lineal de las características \(X_i\) y un error \(u_i\): \[\nu_i=X_i'\gamma+u_i\]
donde se asume que \(E(\nu_i|X_i)=X_i'\gamma\) y donde \(u_i\) y \(X_i\) no están correlacionados
- Si se cumple el SIC, entonces:
\[ \begin{aligned} E(f_i(s)|X_i,s_i)=E(f_i(s)|X_i)&=\alpha+\rho s+E(\nu_i|X_i) \\ &=\alpha+\rho s + X_i'\gamma \end{aligned} \]
Es decir, en el modelo de regresión causal \(Y_i=\alpha+\rho s_i+ X_i'\gamma+u_i\), \(u_i\) no está correlacionado con los regresores \(X_i\) y \(s_i\)
\(\rho\) es el efecto causal de interés
El supuesto clave es que la única razón por la cual \(\nu_i\) y \(s_i\) están correlacionados es \(X_i\)
En resumen
Las comparaciones observacionales están contaminadas por el sesgo de selección
La aleatorización resuelve el problema de selección, es decir, al comparar la variable de resultados de interés entre individuos tratados y no tratados, obtenemos el efecto causal
La FEC nos ayuda a describir la relación entre dos variables, por ejemplo, entre el estado de tratamiento y la variable de resultados
La regresión es una aproximación lineal a la FEC, aún cuando la FEC no sea lineal
Usaremos regresión como una herramienta para comparar la variable de resultados entre grupos
La regresión tiene una interpretación causal si la FEC que trata de aproximar es cauusal
El SIC le da una interpretación causal a la regresión, pero el SIC es un supuesto fuerte
Material de clase en versión preliminar.
No reproducir, no distribuir, no citar.
