Control sintético
Centro de Investigación y Docencia Económicas División de Economía
Motivación
Hasta ahora hemos usado situaciones en las que varios individuos resultan tratados y varios resultan no ser tratados
Los métodos no experimentales nos permiten identificar el efecto de un tratamiento por medio de supuestos
Tratamos de aproximar una situación experimental
Los estudios de evento ocurren cuando una política o programa se lleva a cabo a nivel agregado y afecta a unas pocas (a veces una) unidades
Partimos del concepto de DID
Consideremos un modelo simple de diferencia en diferencias
Observamos una unidad tratada y una que nunca lo fue antes y después del tratamiento
Bajo ciertos supuestos, el estimador de DID es el efecto del tratamiento
La implementación consiste en comparar la unidad tratada con una o varias no tratadas
¿Cuál es el efecto de la inmigración en los mercados laborales?
Card (1990) empleó datos a nivel individual sobre salarios y empleo en el área metropolitana de Miami y los comparó con el promedio de otras cuatro ciudades con proporciones similares de hispanos y negros
Al comparar las tendencias en empleo y salarios con las de este conjunto de ciudades Card concluye que la llegada de inmigrantes no tuvo ningún efecto negativo
Los marieles
![]()
Fuente: Tomada de internet
Los marieles
¿Cuál es el efecto de la inmigración en los mercados laborales?
Card (1990) empleó datos a nivel individual sobre salarios y empleo en el área metropolitana de Miami y los comparó con el promedio de otras cuatro ciudades con proporciones similares de hispanos y negros
Se compara a Miami con el promedio de Atlanta, Houston, Los Angeles y Tampa
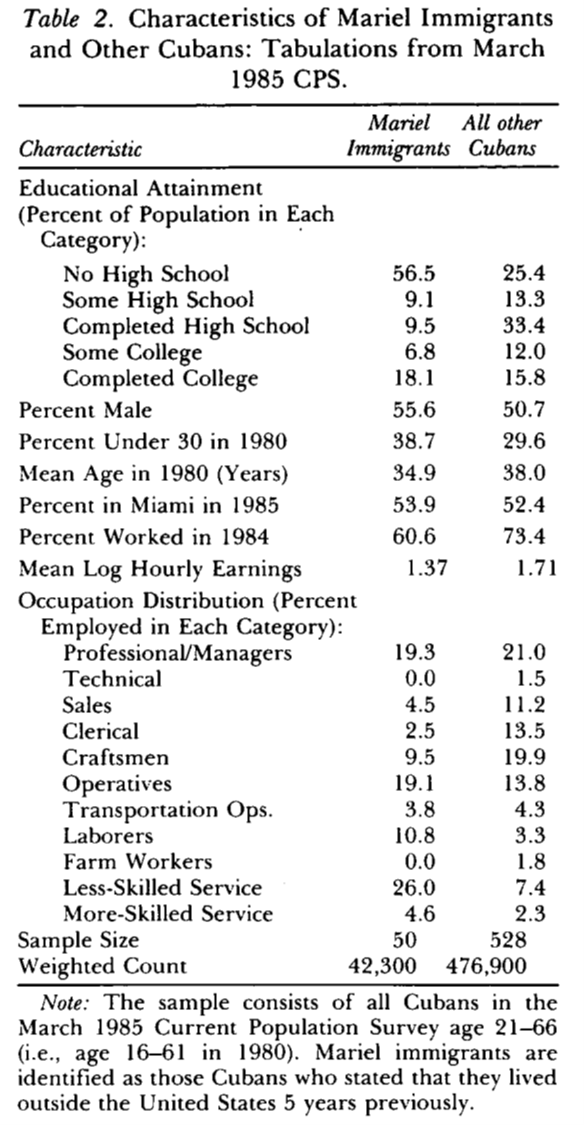
Los marieles
![]()
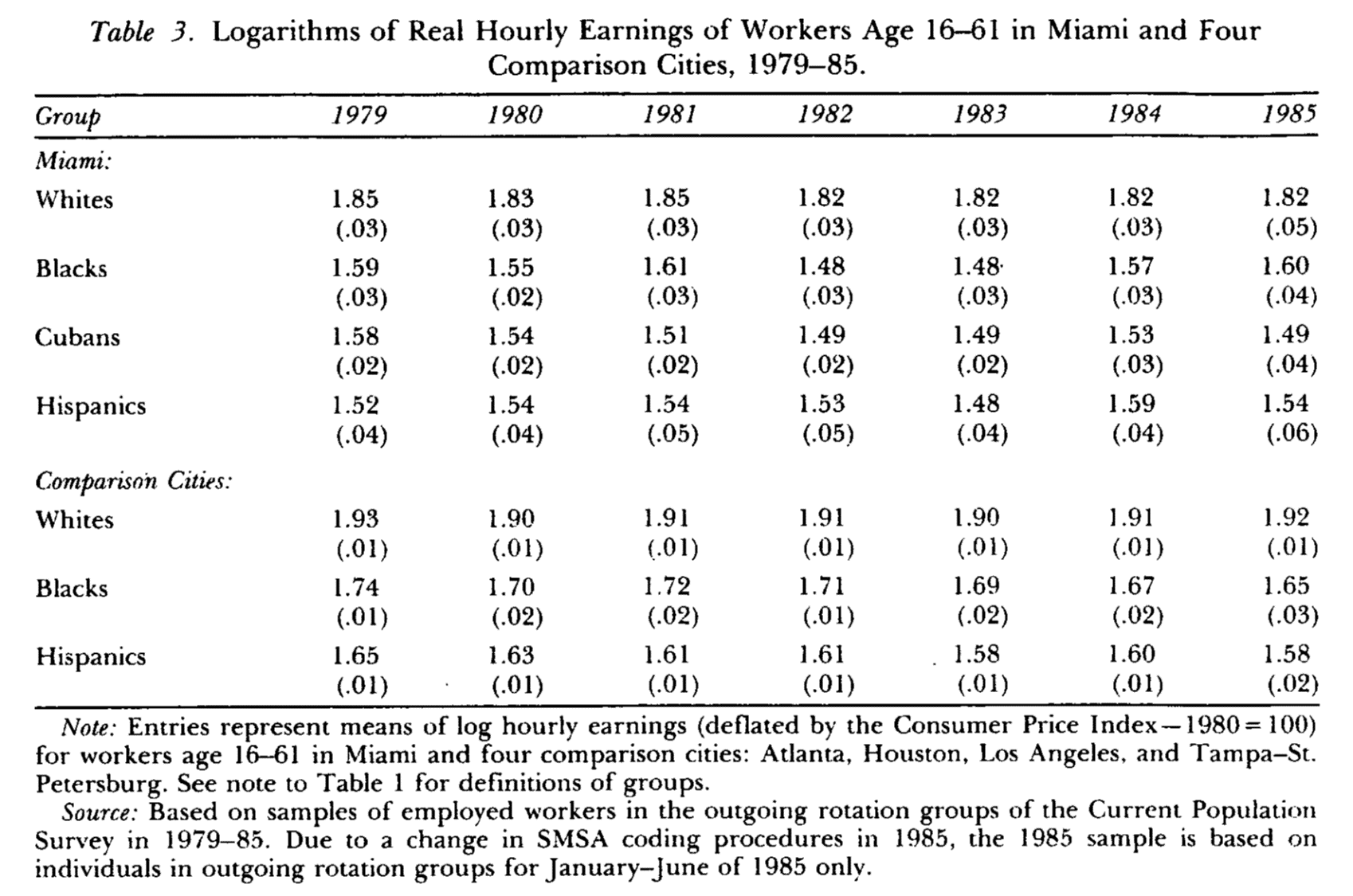
Fuente: Card (1990)
Los marieles
![]()
Fuente: Card (1990)
Los marieles
Al comparar las tendencias en empleo y salarios con las de este conjunto de ciudades Card concluye que la llegada de inmigrantes no tuvo ningún efecto negativo
Tampoco encuentran evidencia de que la distribución de ingresos de los no cubanos se hubiera hecho más desigual
Tampoco hubo efectos concentrados en los grupos menos educados
Se concluye que Miami tuvo la capacidad para absorber el choque de oferta de trabajo sin efectos en el resto del empleo
Otro ejemplo clásico de DID
El ejemplo clásico del modelo de DID es el estudio del efecto del salario mínimo en el empleo
Card y Krueger (1994) comparan los niveles de empleo en restaurantes de comida rápida en Nueva Jersey y Filadelfia
La intuición es que estas dos áreas eran muy similares antes de la subida del salario mínimo en Nueva Jersey
Por lo tanto, comparando las variables de resultados entre ciudades, antes y después de la subida del salario mínimo, podemos obtener el efecto del tratamiento
Los autores no encuentran evidencia de que la subida del salario mínimo redujera el empleo
Crítica a DID
¿Cómo escogemos las unidades de comparación?
¿Cómo podemos saber qué tan buena es la unidad de comparación como contrafactual para reproducir lo que le hubiera pasado a la unidad tratada de no haber recibido el tratamiento?
Extender DID sistemáticamente
El CS permite estudiar sistemáticamente estudios de eventos
En otras ciencias sociales los estudios de eventos regularmente se realizan mediante un análisis detallado de las condiciones institucionales, políticas e históricas de la unidad tratada
El CS nos permite seleccionar sistemáticamente las unidades de comparación
Con las características de las unidades no tratadas se construye una unidad sintética que se emplea para compararla con la unidad tratada y medir el efecto del tratamiento
Se trata de crear una unidad sintética que representa a la unidad tratada como si no hubiera recibido el tratamiento
¿Lo único que podemos hacer son estudios cualitativos?
![]()
El modelo
Tenemos \(J+1\) unidades, siendo \({2,...,J+1}\) las no tratadas
\(t=1,...,T\) periodos
En \(T_0\) ocurre una intervención que solo afecta a \(1\)
\(Y_{it}^I\) es un individuo intervenido, \(Y_{it}^N\) es un individuo no intervenido
Asumimos que antes de la intervención, ninguna unidad fue afectada: \(Y_{it}^N=Y_{it}^I \quad \forall i,t < T_0\)
El efecto del tratamiento en es:
\[\alpha_1=\left(\alpha_{1T_0+1},..., \alpha_{1T}\right)\]
con \(t>T_0\) y \(\alpha_{1t}=Y_{1t}^I-Y_{1t}^N\)
El modelo
- Consideremos un modelo bastante general para la variable de interés (modelo de factores):
\[Y_{it}^N=\delta_t+\theta_t Z_i + \lambda_t\mu_i+\varepsilon_{it}\]
\(Z_i\) son variables no afectadas por la intervención
\(\theta_t\) es un vector de parámetros (que varía en el tiempo)
\(\delta_t\) son factores comunes desconocidos (efectos temporales en un modelo de panel)
\(\mu_i\) es un vector de factores no observados (unknown loadings)
\(\lambda_t\) son factores comunes no observables
DID ocurre cuando \(\lambda_t=\lambda\)
El modelo
Considere una matriz de pesos \(W=\left(w_2,...,w_{J+1}\right)\), con \(w_j \geq 0 \quad \forall j\geq 2\)
Los pesos están normalizados, \(w_2+\ldots+w_{J+1}=1\)
Cada valor de \(W\) representa un potencial CS, es decir, un promedio ponderado de las unidades no tratadas
La variable de resultados para un CS (definido por \(W\)) es:
\[
\begin{aligned}
Y_{Wt}^N&=\sum_{j=2}^{J+1} w_j Y_{jt}= \\
&=\delta_t+\theta_t \left(\sum_{j=2}^{J+1} w_j Z_j\right) + \lambda_t \left(\sum_{j=2}^{J+1} w_j \mu_j \right) + \left(\sum_{j=2}^{J+1} w_j\varepsilon_{jt} \right)
\end{aligned}
\]
- Hay una infinidad de CS, pues hay una infinidad de maneras de asignar los pesos a las unidades no tratadas
El control sintético replica el contrafactual
Suponga que existe una matriz \(W^*\) tal que el CS replica la unidad tratada antes de la intervención
Esto es, el control sintético replica la variable de resultados pre-intervención
\[\sum_{j=2}^{J+1} w^*_j Y_{jt}=Y_{1t} \quad \forall t\in{1,...,T_0}\] - Y replica las características no afectadas por la intervención
\[\sum_{j=2}^{J+1} w^*_j Z_j=Z_1\]
Abadie, Diamond y Hainmueller (2010) dan las condiciones bajo las que el control sintético replica el contrafactual no observado, es decir, \(E\left(Y^N_{1t}-\sum_{j=2}^{J+1} w^*_j Y_{jt}\right)=0\)
Una de estas condiciones es tener suficientes periodos pre-intervención
Por tanto, el efecto del tratamiento puede estimarse como:
\[\hat{\alpha}_{1t}=Y_{1t}-\sum_{j=2}^{J+1} w^*_j Y_{jt}=Y_{1t}-Y_{W^*t}\] para \(t\in \{T_0+1,\ldots,T\}\)
Estimación
Necesitamos datos de panel pre y post intervención para la variable dependiente
Necesitamos algunos puntos pre intervención para las variables \(Z\)
Requerimos suficientes periodos pre intervención para asegurarnos que el CS replica bien a la unidad tratada antes de la intervención
¿Cómo escogemos los pesos \(W\)?
Estimación
Definamos \(X_1=(Z_1',\tilde{Y}_1^{K_1},\ldots,\tilde{Y}_1^{K_M})\) el vector que colecciona las características de la unidad tratada preintervención
En el vector \(X_1\) permitimos que haya \(M\) combinaciones lineales de la variable de resultados pre-intervención
Una combinación lineal de la variable de resultados pre-intervención es
\[\tilde{Y}_i^K=\sum_{s=1}^{T_0}k_sY_{is},\quad\quad K=(k_1,\ldots,k_{T_0})'\]
Por ejemplo, podemos incluir el valor de la variable de resultados en algunos años pre-intervención o el promedio de todos los años pre-intervención
Tenemos lo mismo, pero para las unidades no tratadas, en la matriz \(X_0\)
Definimos \(X_1-X_0W\) como una medida de discrepancia entre \(X_1\) y \(X_0W\)
Estimación de pesos
- Planteamos entonces una función objetivo para minimizar las discrepancias
\[\min_{W\in\mathcal{W}}(X_1-X_0W)V'(X_1-X_0W)\] donde \(V\) es una matriz positiva definida
La solución a este problema, \(W^*(V)\) depende de \(V\)
\(V\) es una matriz de pesos que refleja la importancia relativa de las variables en \(X_1\) y \(X_0\)
Siguiendo a Abadie & Gardeazabal (2003), podemos realizar un proceso que minimice la distancia entre el valor observado de la variable de resultados y el el contrafactual definido por \(W^*(V)\)
Estimación de pesos
Definamos \(\mathcal{Y_1}\) como el vector de variables de resultados en la unidad tratada para los periodos pre-intervención y \(\mathcal{Y_0}\) a la matriz de las mismas variables para los no tratados
Entonces, podemos encontrar la \(V\) óptima como
\[V^*=\arg\min_{V\in\mathcal{V}}(\mathcal{Y}_1-\mathcal{Y}_0W^*(V))'(\mathcal{Y}_1-\mathcal{Y}_0W^*(V))\]
- Y entonces, los pesos para el control sintético estarán dados por \(W^*(V^*)\)
Aplicación: la proposición 99 en California
La proposición 99 en California
En 1988 se pusieron en marcha una serie de medidas en el estado de California para tratar de reducir el consumo de tabaco
Las medidas incluyeron nuevos impuestos, campañas publicitarias, establecimiento de espacios libres de humo, etc.
Para conocer el impacto de la medida en el consumo per cápita, Abadie, Diamond y Hainmueller (2010) construyen un CS
¿Qué pasaría si comparamos California con el resto de los estados de EUA?
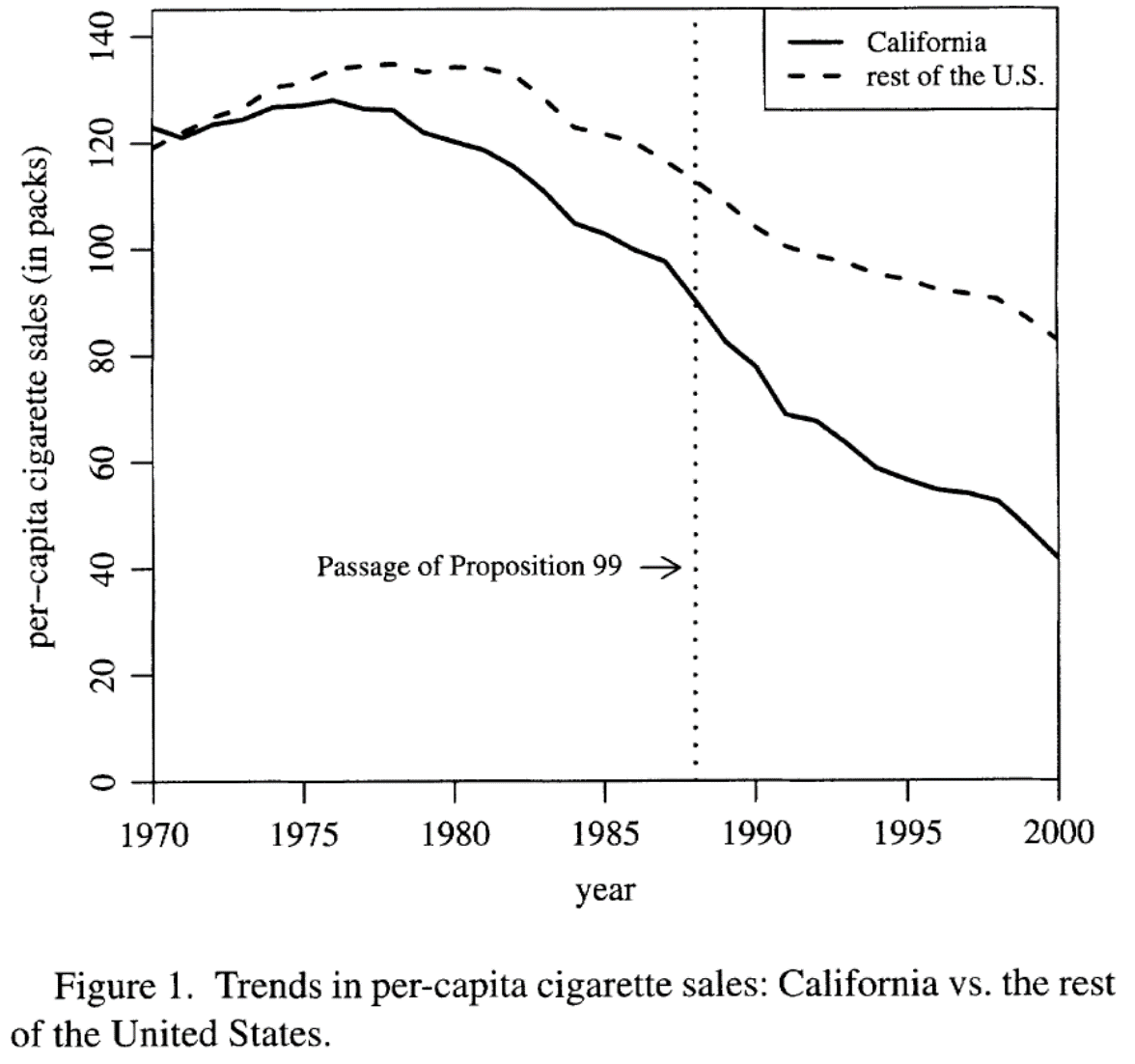
Resultados
Comparar a California con el resto de los estados no es lo más apropiado
El consumo de tabaco ya venía cayendo en todo el país, pero en California la tendencia era más pronunciada
La implementación del CS consiste en escoger a los estados no tratados de forma que puedan reproducir el comportamiento de California antes de la Proposición 99
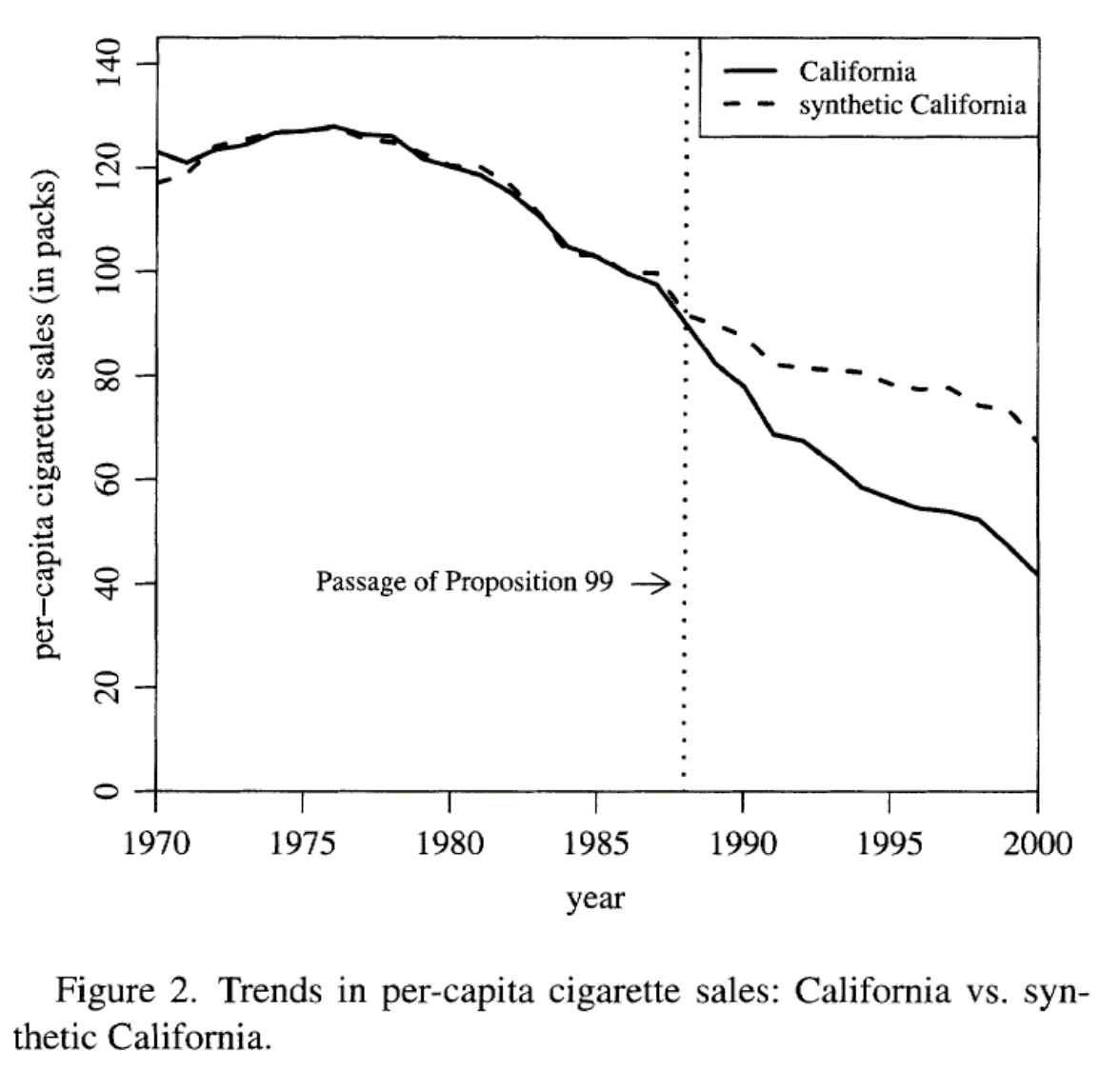
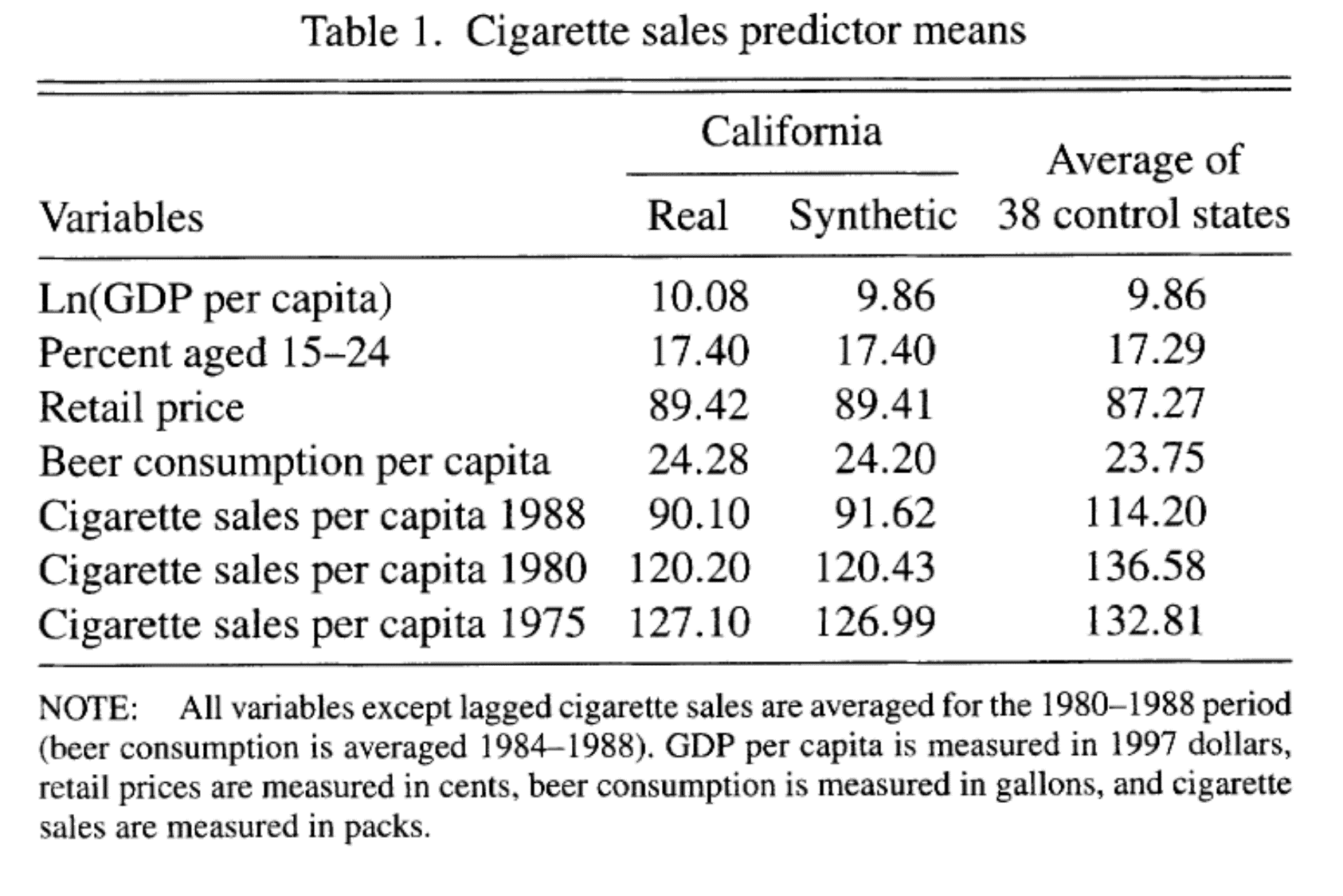
El CS se parece más a California
- Al escoger los pesos apropiadamente el CS es más parecido a California que lo que era el promedio de todos los demás estados
Pesos estimados
El control sintético se caracteriza por una matriz de pesos
Muchas unidades no contribuyen para la construcción del contrafactual
Tenemos un método que nos permite asignar estos pesos de sistemática y dando más peso a los estados más parecidos a California
![]()
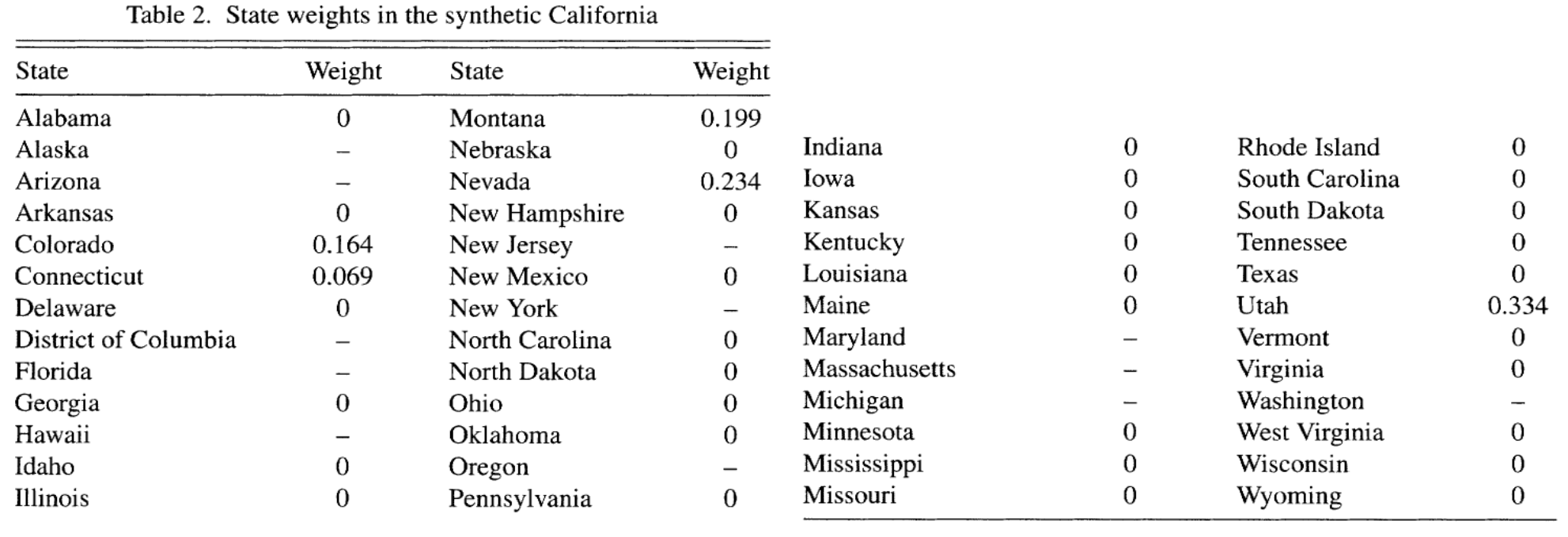
Fuente: Abadie, Diamond y Hainmueller (2010)
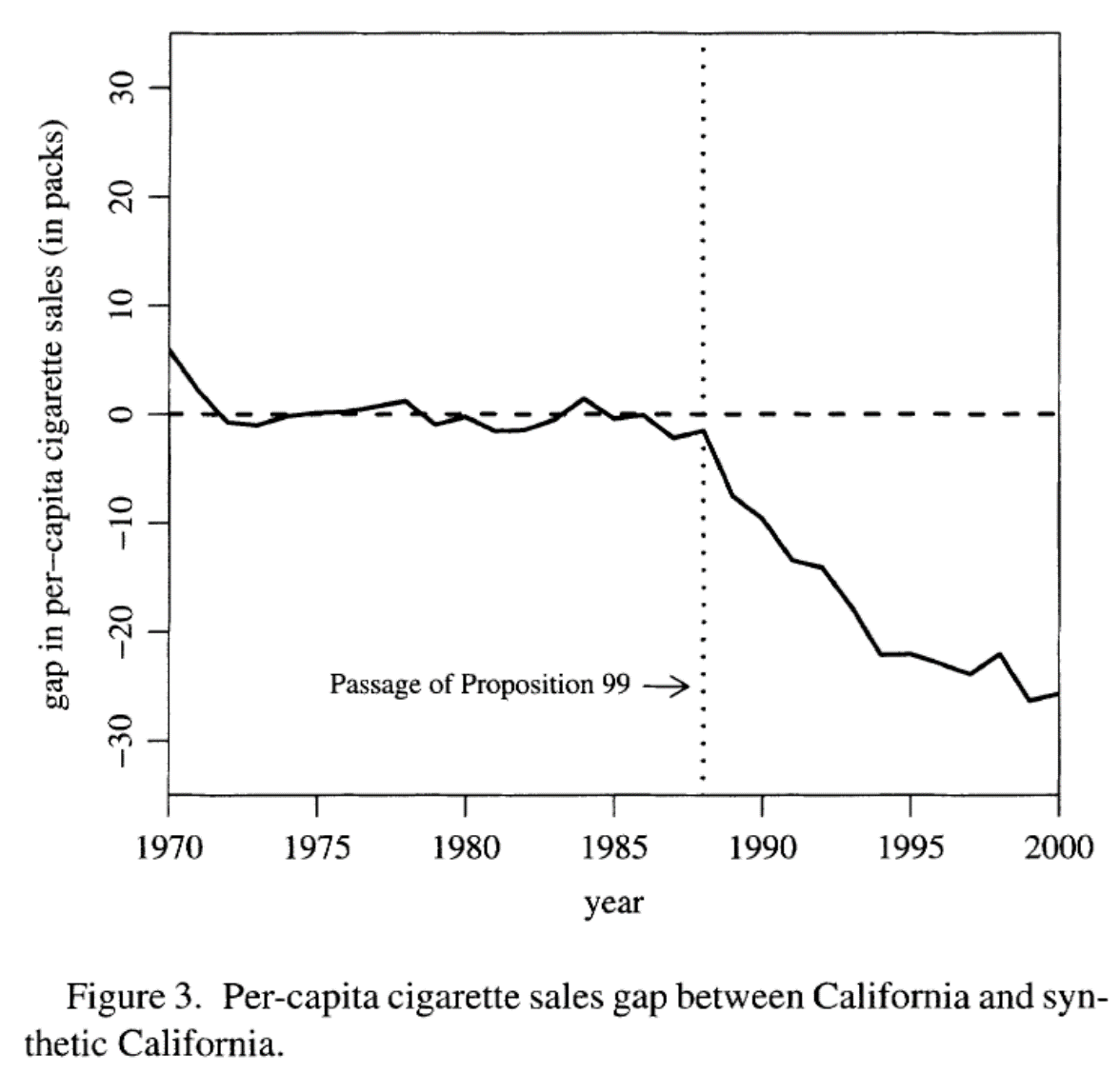
Efecto del tratamiento
El efecto del tratamiento está dado por la diferencia entre el consumo per cápita de cigarrillos en California y el del CS
Esto es la distancia vertical entre las curvas
Al graficar las diferencias obtenemos una gráfica más clara del efecto del tratamiento
Inferencia
A diferencia de las técnicas basadas en regresión, aquí no tenemos errores estándar para hacer inferencia sobre si las diferencias son estadísticamente significativas
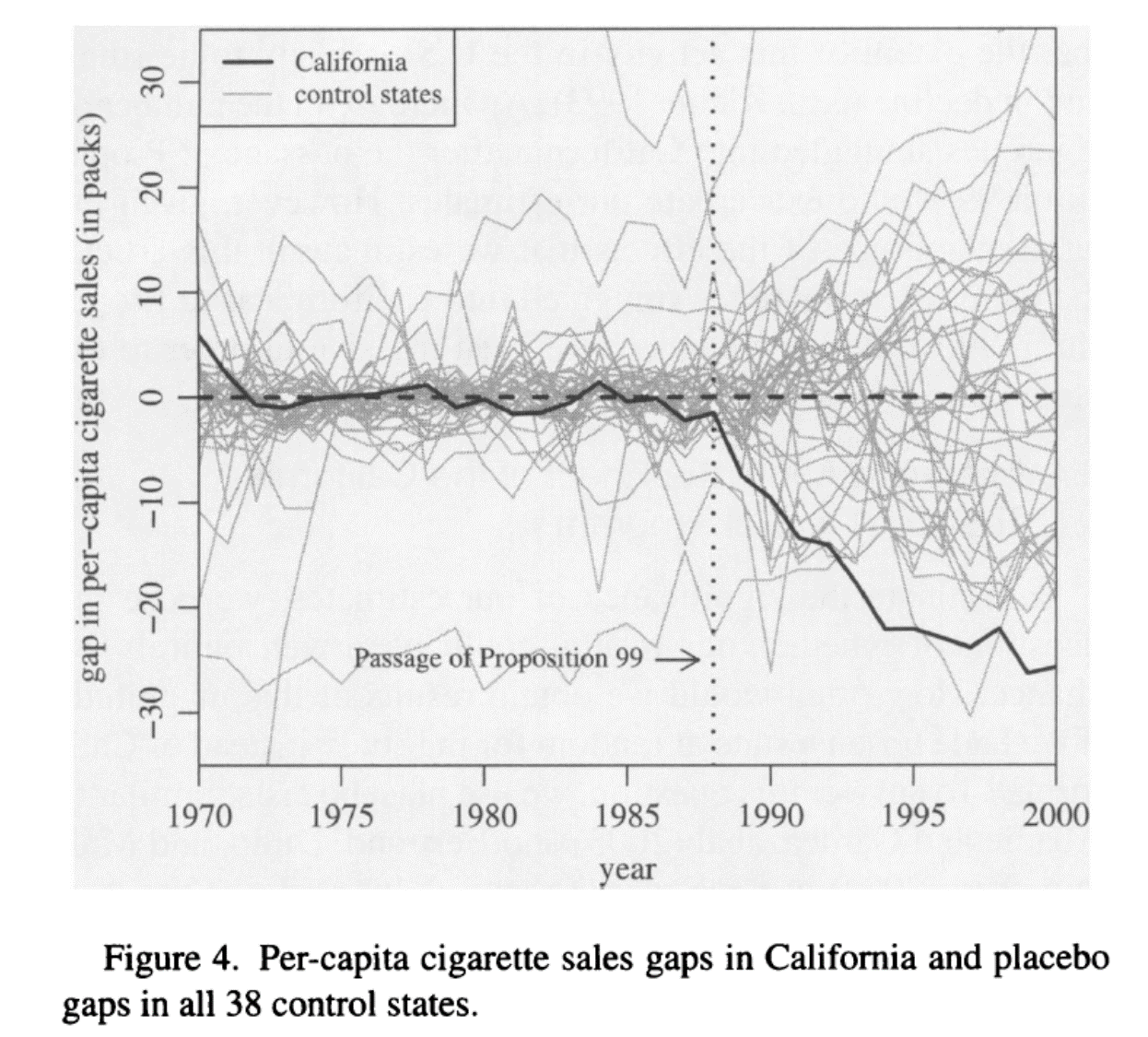
Se propone hacer inferencia basada en placebos
Para cada estado podemos estimar su CS
Es una prueba placebo porque sabemos que para los demás estados no pasó una ley similar a la Proposición 99
Para cada placebo obtenemos una gráfica del efecto del tratamiento como la anterior, aunque sabemos que este efecto debería ser cercano a cero
Inferencia
- Analizamos qué tan común es ver efectos de la magnitud del encontrado con el CS de California
Error de predicción cuadrado medio (MSPE)
\[ratio_{j}^{MSPE}=\frac{MSPE_{post}}{MSPE_{pre}}\]
- En esta aplicación \(ratio_{CA}^{MSPE}\approx130\)
- Podemos ver la distribución de:
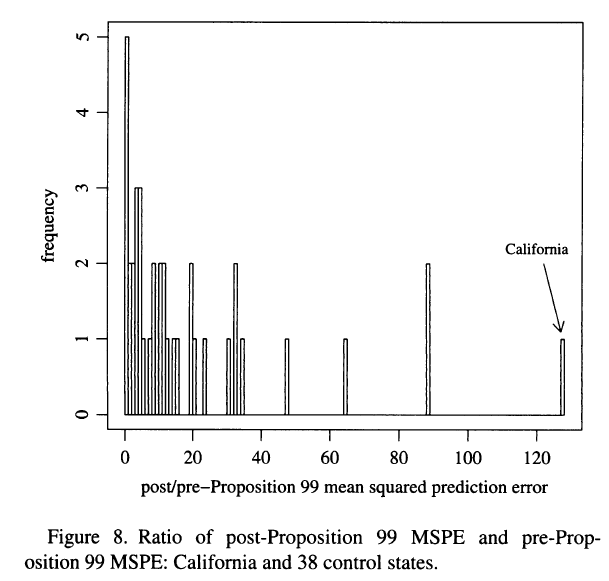
Otros estudios que usan control sintético
La reunificación de Alemania
En 1989 cae el muro de Berlín
Alemania comienza una transición para convertirse en una sola nación
¿Cuál es el efecto de este evento político en la economía de Alemania Occidental?
Abadie, Diamond y Hainmueller (2015) construyen una Alemania sintética a partir de pesos asignados a Austria, Japón, Holanda, Suiza y Estados Unidos
![]()
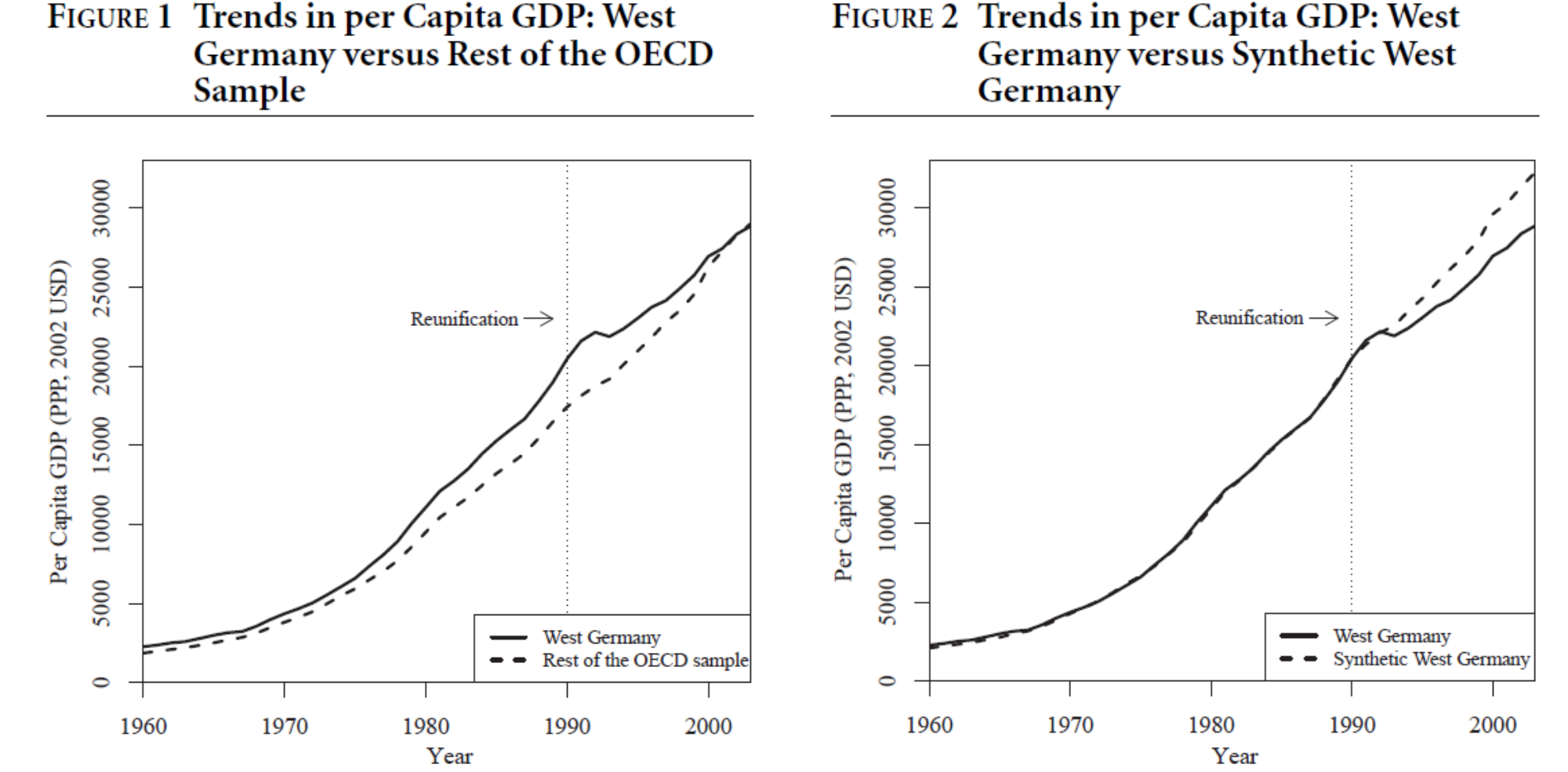
Fuente: Abadie, Diamond y Hainmueller (2015)
El terrorismo en el País Vasco
Desde finales de los 60 ETA comenzó una serie de ataques terroristas
El propósito de ETA era promover la independencia del Estado vasco
Usando características económicas de otras regiones de España se construye un CS
Se estima hasta en % 9 del PIB el costo del terrorismo
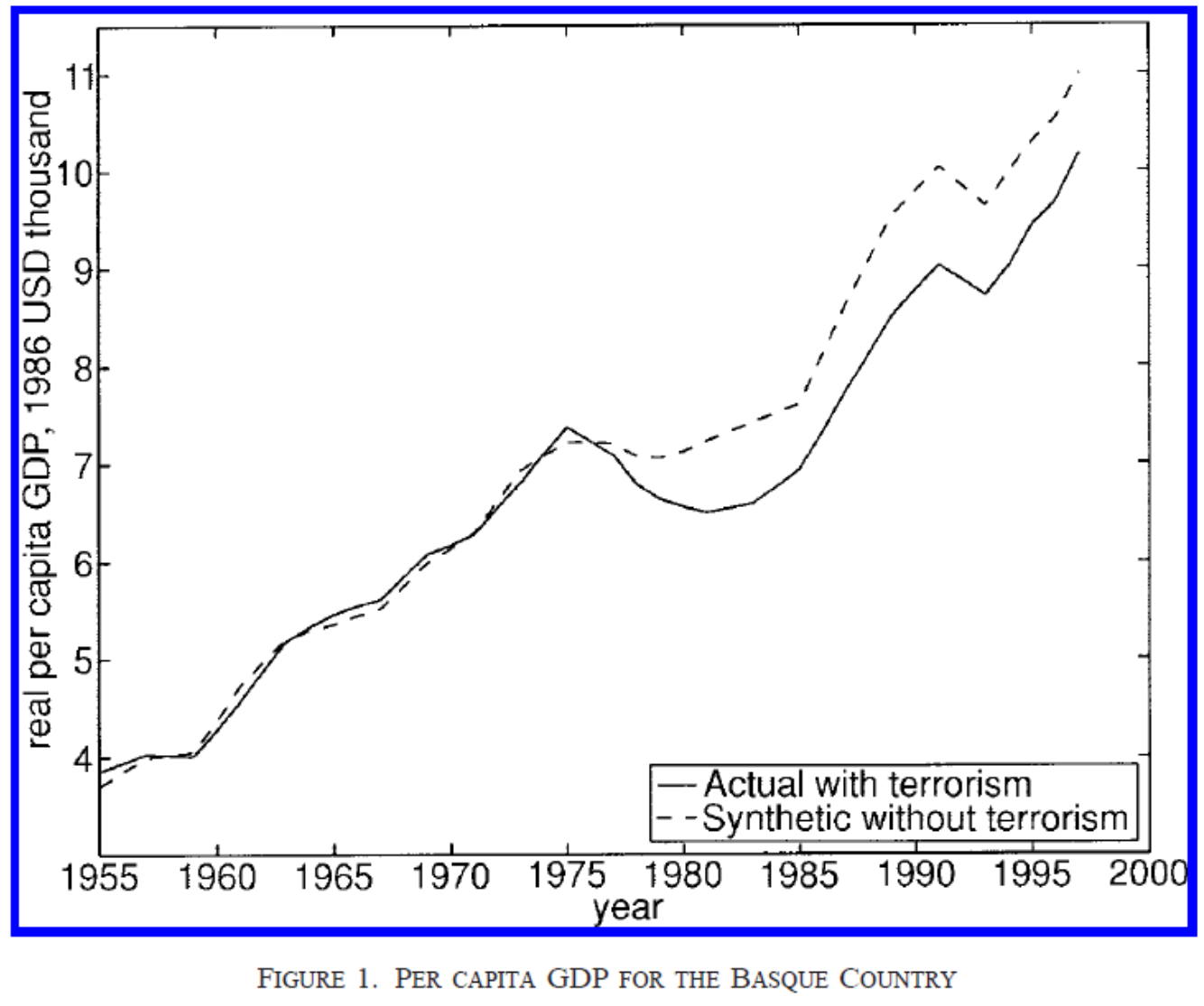
Control sintético con más de una unidad tratada
El valor de las conexiones en tiempos turbulentos
En medio de la crisis financiera de 2008 el entonces presidente Obama nomina a Tim Geithner como Secretario del Tesoro
Justo después de su nombramiento, los rendimientos de muchas empresas en las bolsas mostraron una repentina tendencia a la alza
Semanas después de haberse anunciado, se rumoró que un problema de impuestos podría impedirle a Geithner tomar el cargo, produciéndose el efecto contrario en el valor de las acciones
Acemoglu et al. (2016) estudian si existe una relación entre las empresas conectadas con Geithner y los precios de las acciones
Control sintético con más de un tratado
Los autores identifican las empresas conectadas con Geithner
De alrededor de 600 empresas en la muestra empleada, los autores identifican 66 con algún tipo de conexión con Geithner
Esto permite construir una unidad sintética para cada una de las unidades tratadas a partir del grupo de donadores
La idea es repetir lo que hemos visto en los ejemplos anteriores pero tantas veces como unidades tratadas existan
Medida de rendimiento anormal acumulado
\[\hat{\phi}(\tau,k)=\frac{\sum_{i\in treatment} \frac{\sum^{k}_{t=0} R_{it}-\hat{R}_{it}}{\hat{\sigma}_i}}{\sum_{i\in treatment} \frac{1}{\hat{\sigma}_i}}\]
con \(\hat{\sigma}_i=\sqrt{\frac{\sum_{t<t_0}(R_{it}-\hat{R}_{it})^2}{T}}\)
- Se encuentran rendimientos anormales en los primeros 10 días de entre 6 y 12%
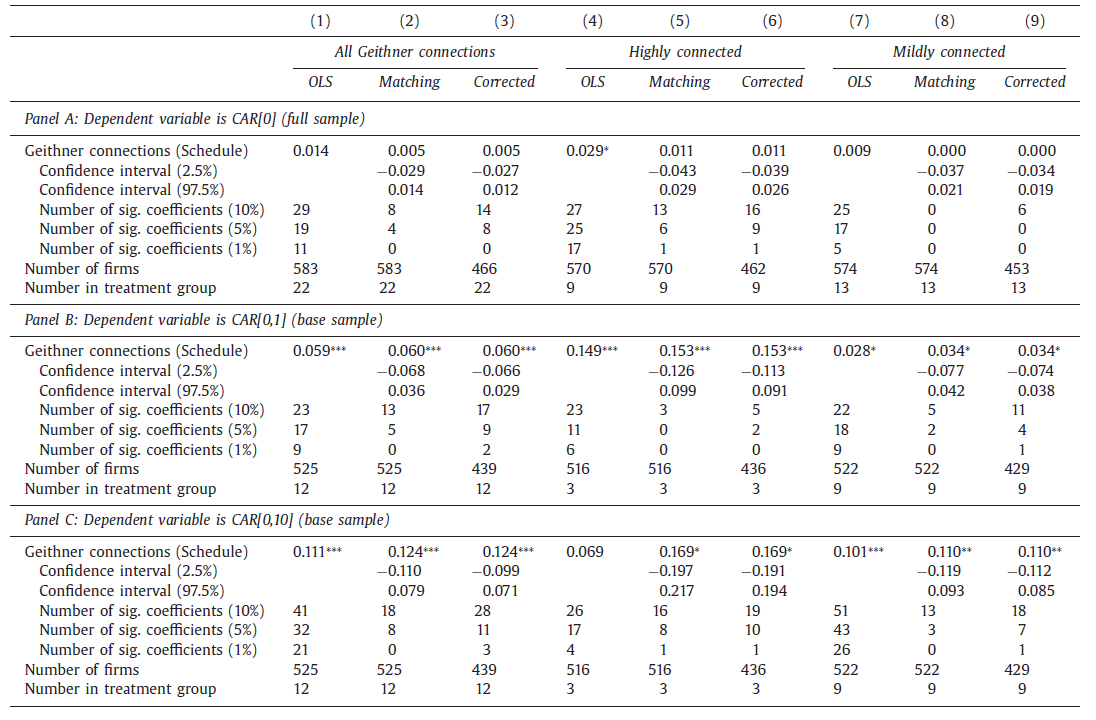
Inferencia
Se obtienen 5 mil remuestreos de grupos de tratamiento placebo del mismo tamaño que el grupo tratado
Se calculan los rendimientos anormales en cada muestra placebo
El efecto estimado es significativo al 5% si no pertenece a al intervalo que contiene los percentiles \([2.5, 97.5]\) de los efectos placebo
Los marieles nuevamente
Parte de la motivación del uso del CS fue el estudio de Card (1990) sobre el impacto de los marieles en la economía de Miami
Criticamos la selección del grupo de comparación
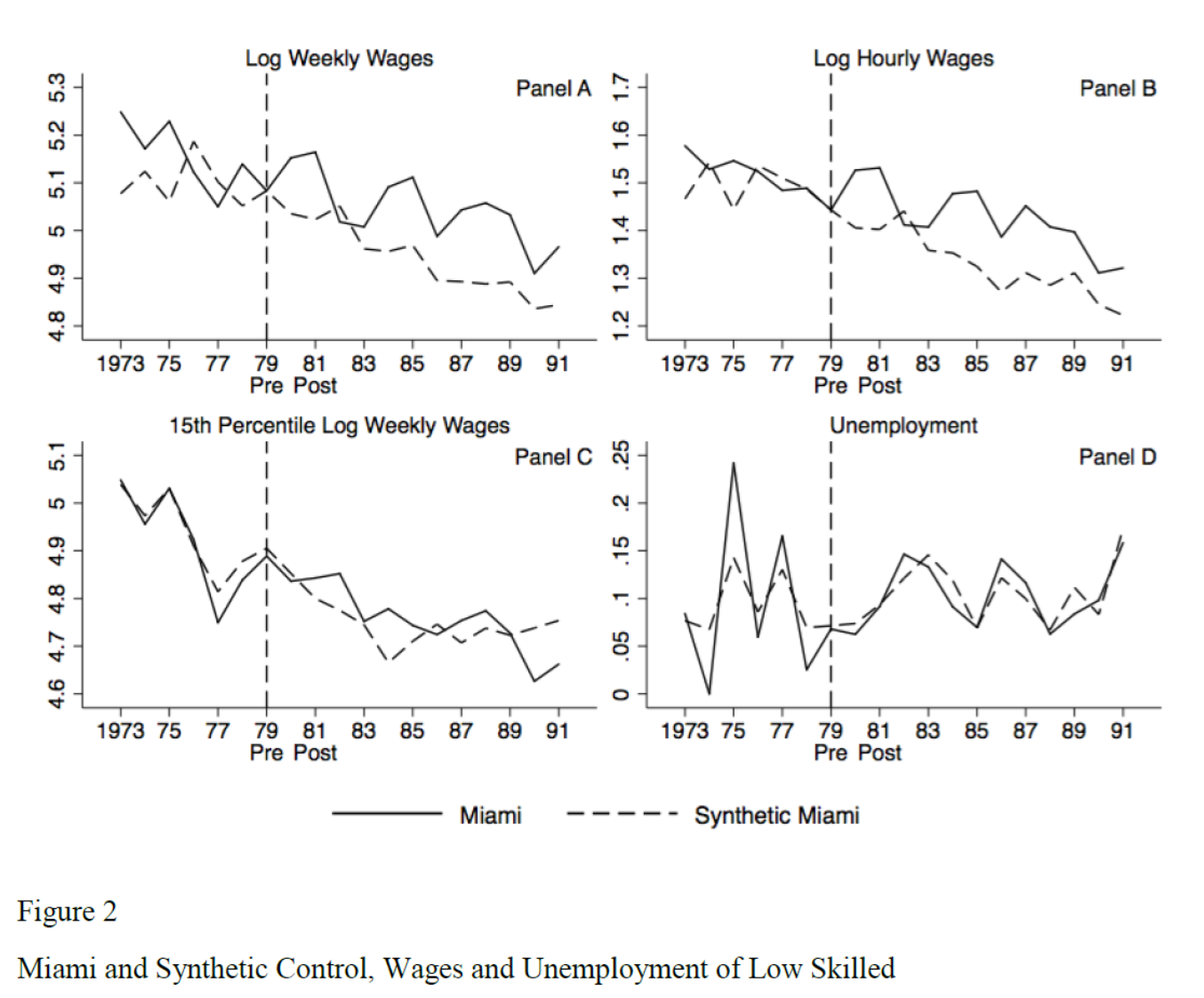
Peri y Yasenov (2018) construyen un Miami sintético para estimar el efecto de los marieles
Muestran que las conclusiones de Card en general se sostienen
Conclusión
La construcción del CS se basa en lo que dicen los datos (data driven) para la selección de las unidades que son usadas y los pesos
El investigador debe ser transparente al mostrar qué tan bueno es el CS que construye
Para construir el CS no se usan los datos post-intervención por lo que, al menos en teoría, el investigador no debería seleccionar el CS guiado por las conclusiones que resultan
Material de clase en versión preliminar.
No reproducir, no distribuir, no citar.
