acafs <- read_csv("../files/ehec_data.csv")
table(filter(acafs,year==2018)$yexp2)
2014 2015 2016 2017 2019 Inf
22 3 2 1 2 16 Los datos en ehec_data.csv son datos de panel a nivel estado para los Estados Unidos de 2008 a 2019. A partir de 2014 se llevó a cabo un proceso de expansión de un programa de ayuda para subsidiar el costo de los servicios de salud de personas de bajos ingresos, Medicaid Expansion. La columna yexp2 indica el año en que cada estado es tratado con la expansión del programa, treated es un indicador de si el estado \(i\) es tratado en el año \(t\), mientras que rel_year indica el número de años desde la expansión. Si yexp2==Inf, entonces el estado no ha sido tratado para 2019. Se busca estimar el efecto de la expansión del programa en el porcentaje de la población asegurada que es de bajos ingresos, sin hijos, y de entre 25 y 64 años de edad, dins.
[5 puntos] ¿Por qué decimos que esta es una aplicación de la estimación de efectos de tratamiento con adopción escalonada?
En esta aplicación, cada estado comienza a ser tratado en indistintos momentos del tiempo. Si hacemos un tabulado de yexp2 notamos cuántos estados se vuelven tratados en cada año:
acafs <- read_csv("../files/ehec_data.csv")
table(filter(acafs,year==2018)$yexp2)
2014 2015 2016 2017 2019 Inf
22 3 2 1 2 16 El panel comienza en 2008. 22 estados son tratados desde 2014, 3 en 2015 y así sucesivamente. 16 estados nunca son tratados.
[5 puntos] Como punto de partida, estime el efecto del tratamiento sobre dins usando efectos fijos por estado y año (TWFE) y empleando una librería específica para efectos fijos, como felm. Tome en cuenta la agrupación de los errores. Interprete sus resultados.
Usando felm podemos incorporar ya el nivel de agrupación de los errores:
twfe <- felm(dins ~ treated | stfips + year | 0 | stfips,
data = acafs)
modelsummary(twfe,
coef_map = c('treated'),
stars = c('*' = .1, '**' = .05, '***'= 0.01),
gof_map = c('nobs'),
output = 'gt')| (1) | |
|---|---|
| treated | 0.070*** |
| (0.007) | |
| Num.Obs. | 552 |
| * p < 0.1, ** p < 0.05, *** p < 0.01 | |
[5 puntos] Compruebe que puede obtener el mismo resultado con una regresión lineal usando el paquete lm e incluyendo, además de la variable de tratamiento, dummies de estado y de año.
Estimamos con dummies:
m1 <- lm(dins ~ treated + factor(stfips) + factor(year),
data = acafs)Luego presentamos con errores clásicos y errores agrupados:
modelsummary(list(m1, m1),
coef_map = c('treated'),
vcov=list(NULL, clubSandwich::vcovCR(m1, type='CR1', cluster=acafs$stfips)),
stars = c('*' = .1, '**' = .05, '***'= 0.01),
gof_map = c('nobs'),
output = 'gt')| (1) | (2) | |
|---|---|---|
| treated | 0.070*** | 0.070*** |
| (0.004) | (0.007) | |
| Num.Obs. | 552 | 552 |
| * p < 0.1, ** p < 0.05, *** p < 0.01 | ||
[10 puntos] Ahora muestre que podemos obtener el coeficiente de TWFE a partir de una regresión bivariada entre el porcentaje de la población asegurada y treated, una vez purgada por efectos fijos. Para ello, primero estime una regresión de treated en función de los efectos fijos. Obtenga la predicción y luego defina una nueva variable igual a la diferencia entre treated y la predicción que acaba de obtener. Finalmente, obtenga el coeficiente de TWFE con una regresión del porcentaje de la población asegurada en función de la diferencia antes definida.
Corremos la primera regresión para purgar los efectos fijos:
d1 <- lm(treated ~ factor(stfips) + factor(year),
data = acafs)Definimos la nueva variable:
acafs <- acafs %>%
mutate(treated_hat = treated-predict(d1))Y finalmente estimamos:
summary(m2 <- lm(dins ~ treated_hat,
data = acafs))
Call:
lm(formula = dins ~ treated_hat, data = acafs)
Residuals:
Min 1Q Median 3Q Max
-0.225383 -0.066374 0.001295 0.069099 0.200551
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.699824 0.003744 186.909 < 2e-16 ***
treated_hat 0.070321 0.014475 4.858 1.55e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.08797 on 550 degrees of freedom
Multiple R-squared: 0.04115, Adjusted R-squared: 0.0394
F-statistic: 23.6 on 1 and 550 DF, p-value: 1.547e-06Obtenemos el mismo coeficiente. Frisch–Waugh–Lovell tenían razón:
modelsummary(list(m2),
coef_map = c('treated_hat'),
stars = c('*' = .1, '**' = .05, '***'= 0.01),
gof_map = c('nobs'),
output = 'gt')| (1) | |
|---|---|
| treated_hat | 0.070*** |
| (0.014) | |
| Num.Obs. | 552 |
| * p < 0.1, ** p < 0.05, *** p < 0.01 | |
[10 puntos] Realice la descomposición de Goodman-Bacon (2021). Construya un gráfico donde muestre en el eje \(x\) el peso otorgado a cada comparación 2x2 y en el eje \(y\) el efecto estimado correspondiente a cada comparación. Interprete el gráfico obtenido.
Como vimos en clase:
#Goodman-Bacon decomposition
df_bacon <- bacon(dins ~ treated,
data = acafs,
id_var = "stfips",
time_var = "year") type weight avg_est
1 Earlier vs Later Treated 0.14911 0.06983
2 Later vs Earlier Treated 0.05827 0.04486
3 Treated vs Untreated 0.79262 0.07228coef_bacon <- sum(df_bacon$estimate * df_bacon$weight)
print(paste("Weighted sum of decomposition =", round(coef_bacon, 4)))[1] "Weighted sum of decomposition = 0.0703"twfe <- feols(dins ~ treated | stfips + year,
data = acafs,
cluster = ~stfips)
#Gráfico
df_bacon %>%
ggplot(aes(x=weight,
y=estimate,
shape=type)) +
geom_point() +
geom_hline(yintercept = round(twfe$coefficients, 4))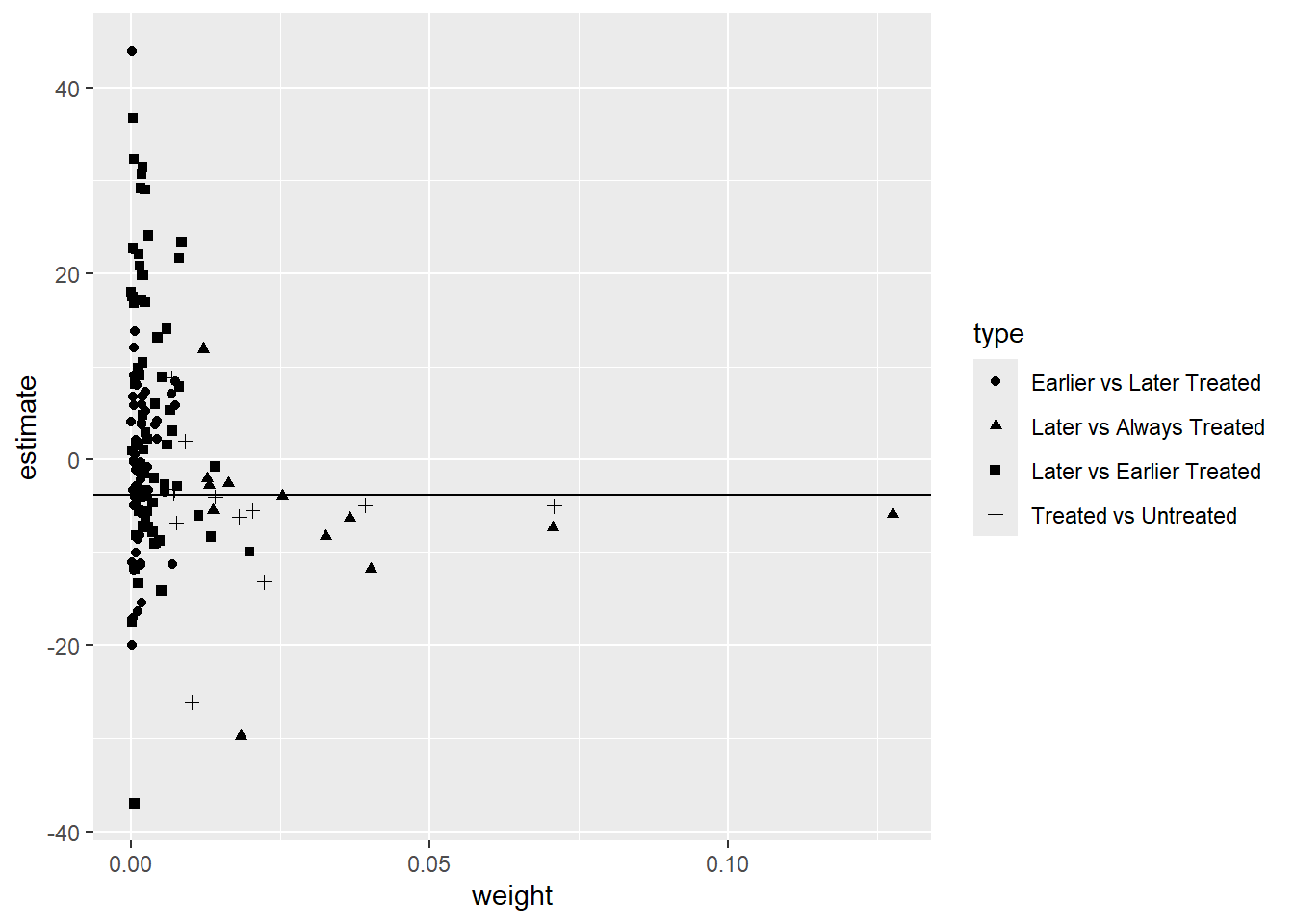
Las comparaciones que más pesan en el estimador de efectos fijos son las de estados tratados con los nunca tratados, que llegan a recibir un peso de más de 0.6. La comparación con más peso tiene un efecto estimado de 0.0749, parecida al 0.07 que se obtiene con efectos fijos.
[10 puntos] Implemente el estimador de Callaway & Sant’Anna (2021) para estimar los efectos del tratamiento específicos para cada cohorte, usando el paquete did. Utilice como grupo de comparación los estados no tratados aún.
acafs <- acafs %>%
mutate(stfips2 = as.numeric(factor(stfips)))
atts_nyt <- att_gt(yname = "dins",
tname = "year",
idname = "stfips2",
gname = "yexp2",
data = acafs,
control_group = "notyettreated",
est_method = 'reg',
bstrap = TRUE,
biters = 1000,
print_details = FALSE,
panel = TRUE)
summary(atts_nyt)
Call:
att_gt(yname = "dins", tname = "year", idname = "stfips2", gname = "yexp2",
data = acafs, panel = TRUE, control_group = "notyettreated",
bstrap = TRUE, biters = 1000, est_method = "reg", print_details = FALSE)
Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
Group-Time Average Treatment Effects:
Group Time ATT(g,t) Std. Error [95% Simult. Conf. Band]
2014 2009 -0.0065 0.0051 -0.0428 0.0298
2014 2010 0.0111 0.0063 -0.0344 0.0566
2014 2011 0.0015 0.0055 -0.0377 0.0407
2014 2012 0.0016 0.0058 -0.0403 0.0436
2014 2013 0.0009 0.0068 -0.0482 0.0500
2014 2014 0.0467 0.0084 -0.0137 0.1071
2014 2015 0.0692 0.0095 0.0013 0.1371 *
2014 2016 0.0785 0.0100 0.0068 0.1502 *
2014 2017 0.0725 0.0101 -0.0003 0.1453
2014 2018 0.0738 0.0118 -0.0112 0.1589
2014 2019 0.0803 0.0102 0.0068 0.1539 *
2015 2009 0.0071 0.0129 -0.0858 0.1000
2015 2010 -0.0245 0.0109 -0.1030 0.0541
2015 2011 -0.0027 0.0057 -0.0434 0.0381
2015 2012 0.0003 0.0035 -0.0250 0.0256
2015 2013 -0.0100 0.0111 -0.0898 0.0699
2015 2014 -0.0020 0.0070 -0.0524 0.0483
2015 2015 0.0491 0.0235 -0.1196 0.2178
2015 2016 0.0526 0.0145 -0.0518 0.1571
2015 2017 0.0682 0.0102 -0.0053 0.1416
2015 2018 0.0663 0.0125 -0.0236 0.1562
2015 2019 0.0738 0.0116 -0.0094 0.1569
2016 2009 0.0022 0.0057 -0.0391 0.0435
2016 2010 0.0511 0.0077 -0.0045 0.1066
2016 2011 -0.0262 0.0075 -0.0802 0.0278
2016 2012 -0.0276 0.0091 -0.0928 0.0377
2016 2013 0.0440 0.0088 -0.0190 0.1071
2016 2014 -0.0322 0.0113 -0.1132 0.0489
2016 2015 0.0409 0.0160 -0.0744 0.1561
2016 2016 0.0317 0.0103 -0.0424 0.1057
2016 2017 0.0368 0.0080 -0.0207 0.0943
2016 2018 0.0645 0.0123 -0.0242 0.1532
2016 2019 0.0825 0.0088 0.0192 0.1458 *
2017 2009 0.0102 0.0025 -0.0075 0.0279
2017 2010 -0.0161 0.0035 -0.0410 0.0087
2017 2011 0.0019 0.0029 -0.0191 0.0228
2017 2012 0.0177 0.0033 -0.0058 0.0412
2017 2013 0.0012 0.0035 -0.0239 0.0264
2017 2014 -0.0063 0.0061 -0.0499 0.0373
2017 2015 0.0036 0.0064 -0.0425 0.0497
2017 2016 0.0398 0.0053 0.0017 0.0780 *
2017 2017 0.0471 0.0054 0.0083 0.0859 *
2017 2018 0.0681 0.0045 0.0356 0.1005 *
2017 2019 0.0650 0.0035 0.0399 0.0901 *
2019 2009 0.0189 0.0053 -0.0192 0.0569
2019 2010 -0.0269 0.0083 -0.0863 0.0326
2019 2011 -0.0244 0.0029 -0.0454 -0.0034 *
2019 2012 0.0024 0.0183 -0.1290 0.1337
2019 2013 0.0129 0.0070 -0.0371 0.0630
2019 2014 0.0003 0.0073 -0.0522 0.0528
2019 2015 -0.0108 0.0090 -0.0756 0.0540
2019 2016 -0.0182 0.0256 -0.2025 0.1660
2019 2017 0.0093 0.0194 -0.1299 0.1485
2019 2018 0.0062 0.0064 -0.0394 0.0518
2019 2019 0.0365 0.0057 -0.0042 0.0773
---
Signif. codes: `*' confidence band does not cover 0
Control Group: Not Yet Treated, Anticipation Periods: 0
Estimation Method: Outcome Regressionggdid(atts_nyt)
[10 puntos] Reporte los resultados agregados obtenidos a partir del estimador Callaway & Sant’Anna (2021), usando una agregación dinámica que muestre los efectos promedio para cada periodo antes y después del tratamiento. Grafique e interprete los resultados.
Graficamos:
agg.es <- aggte(atts_nyt,
type = "dynamic")
summary(agg.es)
Call:
aggte(MP = atts_nyt, type = "dynamic")
Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
Overall summary of ATT's based on event-study/dynamic aggregation:
ATT Std. Error [ 95% Conf. Int.]
0.0688 0.0079 0.0534 0.0843 *
Dynamic Effects:
Event time Estimate Std. Error [95% Simult. Conf. Band]
-10 0.0189 0.0053 0.0052 0.0326 *
-9 -0.0269 0.0086 -0.0492 -0.0046 *
-8 -0.0129 0.0117 -0.0433 0.0176
-7 -0.0014 0.0082 -0.0226 0.0198
-6 0.0189 0.0089 -0.0042 0.0420
-5 -0.0084 0.0053 -0.0220 0.0053
-4 0.0054 0.0079 -0.0151 0.0258
-3 0.0026 0.0048 -0.0099 0.0152
-2 -0.0012 0.0035 -0.0103 0.0078
-1 0.0049 0.0042 -0.0059 0.0158
0 0.0453 0.0064 0.0287 0.0618 *
1 0.0651 0.0081 0.0440 0.0861 *
2 0.0759 0.0081 0.0550 0.0969 *
3 0.0726 0.0094 0.0480 0.0971 *
4 0.0738 0.0107 0.0460 0.1016 *
5 0.0803 0.0103 0.0536 0.1071 *
---
Signif. codes: `*' confidence band does not cover 0
Control Group: Not Yet Treated, Anticipation Periods: 0
Estimation Method: Outcome Regressionggdid(agg.es)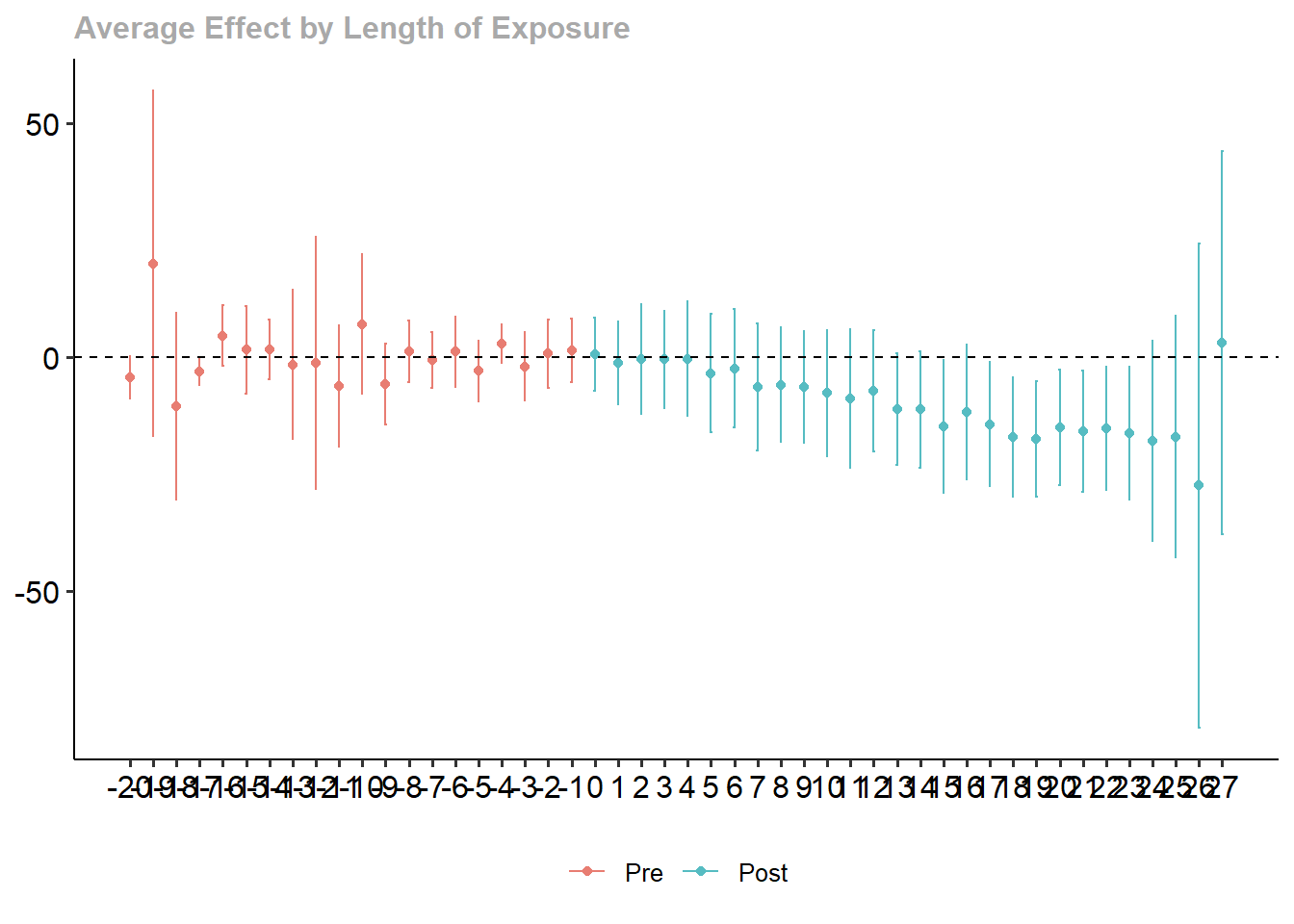
[10 puntos] Reporte los resultados agregados obtenidos a partir del estimador Callaway & Sant’Anna (2021), usando una agregación or grupos que muestre los efectos promedio para cada cohorte del tratamiento. Grafique e interprete los resultados.
Graficamos:
agg.es <- aggte(atts_nyt,
type = "group")
summary(agg.es)
Call:
aggte(MP = atts_nyt, type = "group")
Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
Overall summary of ATT's based on group/cohort aggregation:
ATT Std. Error [ 95% Conf. Int.]
0.0657 0.0106 0.045 0.0864 *
Group Effects:
Group Estimate Std. Error [95% Simult. Conf. Band]
2014 0.0702 0.0089 0.0496 0.0908 *
2015 0.0620 0.0159 0.0251 0.0989 *
2016 0.0539 0.0049 0.0425 0.0652 *
2017 0.0601 0.0039 0.0510 0.0692 *
2019 0.0365 0.0052 0.0245 0.0486 *
---
Signif. codes: `*' confidence band does not cover 0
Control Group: Not Yet Treated, Anticipation Periods: 0
Estimation Method: Outcome Regressionggdid(agg.es)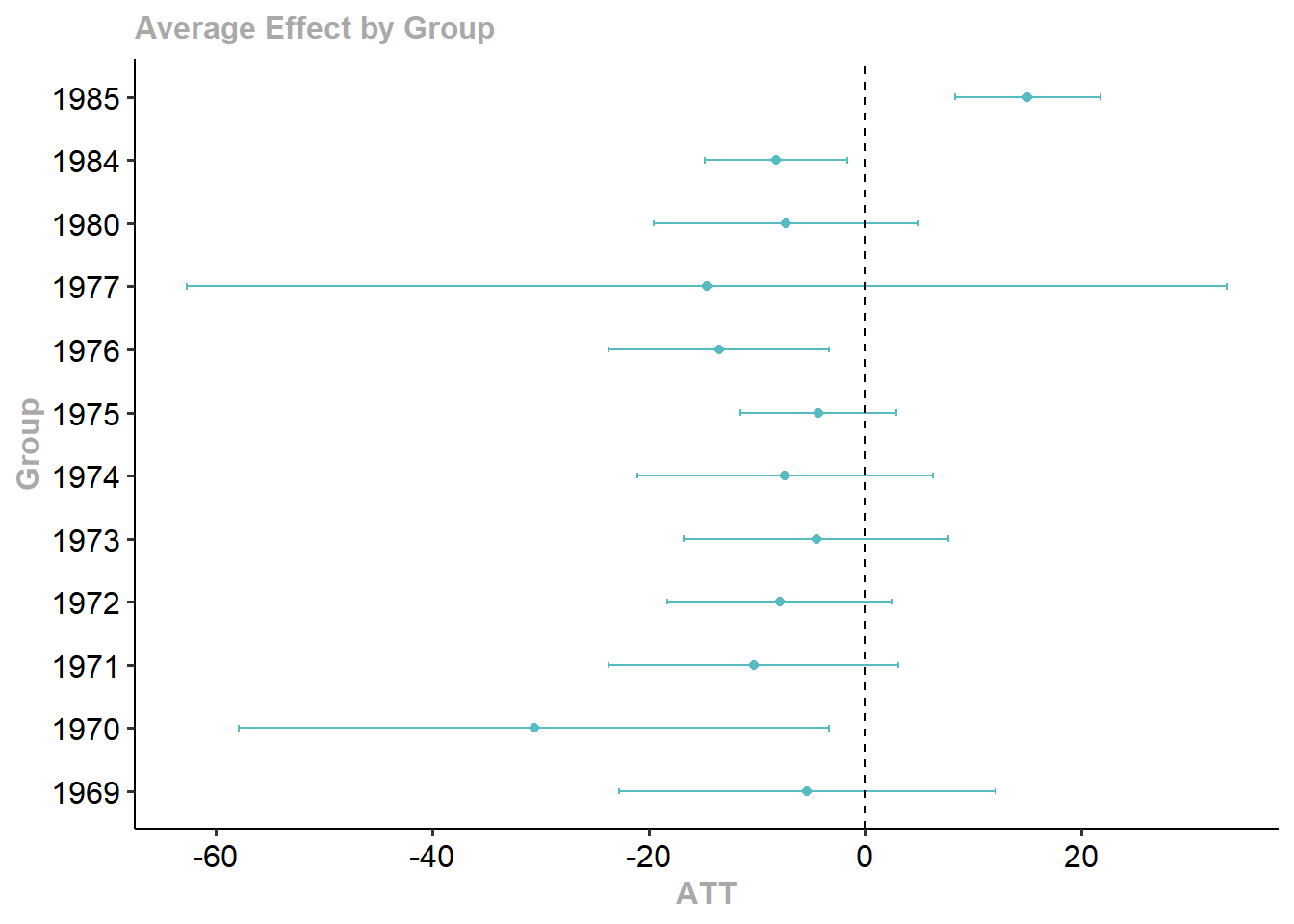
Suponga que se convierte en asesor de un programa de educación. Se tiene la hipótesis de que el bajo aprovechamiento académico responde a las condiciones de desventaja de los alumnos más pobres. Por tanto, el programa otorga una transferencia monetaria a los estudiantes considerados pobres. Para determinar la elegibilidad del programa, la autoridad educativa diseña un cuestionario socioeconómico y crea un índice de riqueza de los hogares. Además, esta entidad establece un umbral por debajo del cual los estudiantes son considerados pobres. Todos los estudiantes considerados pobres reciben una transferencia monetaria que es entregada en efectivo directamente al estudiante.
[5 puntos] ¿Qué aspectos del programa permitirían emplear un diseño de regresión discontinua para evaluar la efectividad de este sobre el desempeño escolar y cómo mostraría su validez empíricamente?
En este caso podemos usar el método de regresión discontinua por las siguientes razones:
i. La variable de selección es continua.
ii. Es estatus de tratamiento es una función determinística de la posición de la variable de selección respecto al umbral.
iii. La probabilidad de recibir el tratamiento es discontinua en el umbral.
iv. Los estudiantes no pueden manipular la riqueza del hogar para posicionarse estratégicamente por encima del umbral.
[10 puntos] ¿Cómo emplearía el diseño de este programa para evaluar su efectividad con un modelo de regresión discontinua nítida? Elabore una gráfica donde explique una situación en la que el programa muestra ser efectivo. Describa cómo usaría una regresión para hacer inferencia respecto a la efectividad del programa.
La forma gráfica de inspeccionar la presencia de una regresión consiste en graficar la variable de resultados en función de la variable de asignación. En este caso, esperaríamos que los estudiantes que están por debajo del umbral tengan una diferencia notable en términos de su desempeño académico si la transferencia se usa para mejorar insumos en el proceso educativo. No era estrictamente necesario simular un proceso para obtener una representación gráfica, pero aquí lo hice así. Quizás esto pueda ser de utilidad para futuras aplicaciones:
set.seed(1711)
riqueza <- runif(1000, -1, 1)
y <- 3 + 1*riqueza - 3*(riqueza>=0) + rnorm(1000, mean = 0, sd = 0.2)
data.sharp <- data.frame(y, riqueza, c = 0)
data.sharp %>%
ggplot() +
geom_point(aes(x=riqueza, y=y), size=0.5, alpha=0.5) +
geom_abline(intercept = 3, slope = 1, linetype = "dashed") +
geom_abline(intercept = 0, slope = 1, linetype = "dashed") +
geom_vline(xintercept = 0) +
xlab("Índice de riqueza")+
ylab("Desempeño")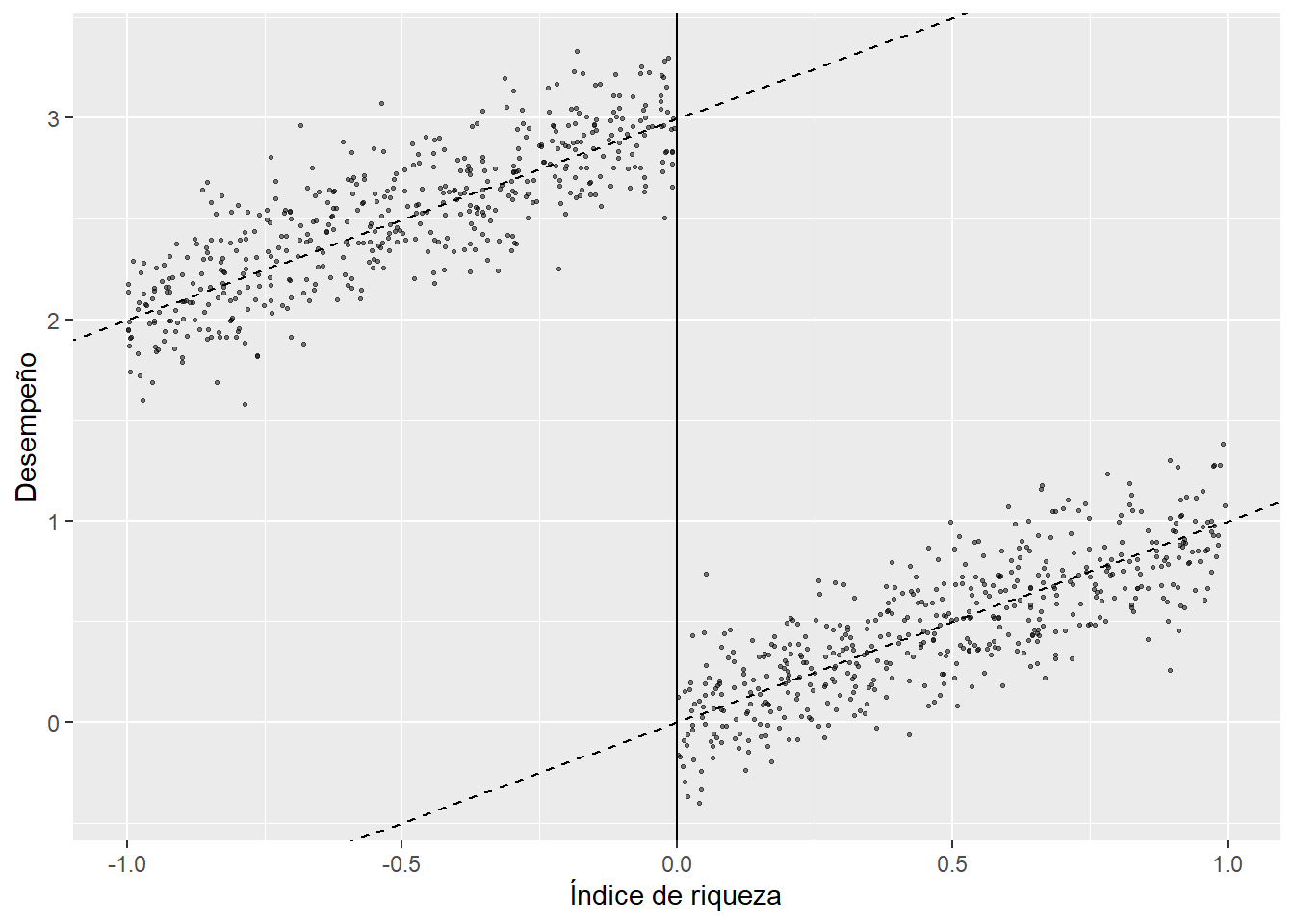
Paramétricamente, la forma más sencilla de identificar el efecto de la discontinuidad es especificando una regresión como sigue:
\[y_i=\alpha+\tau D_i+ \beta x_i+\varepsilon_i\]
donde \(x_i\) es la variable de selección y \(D_i\) es una variable indicadora que toma el valor de uno cuando el índice de riqueza se encuentra por debajo del umbral. Controlar por \(x_i\) captura la relación que tiene la riqueza en el desempeño académico. Se recomiendan al menos dos tipos de procedimientos más para comprobar la robustez de los efectos encontrados.
El primero es incluir un polinomio lo suficientemente flexible de \(x_i\): \[y_i=\alpha+\tau D_i+ Bf(x_i)+\varepsilon_i\]
El segundo consiste en permitir que la pendiente sea diferente antes y después de la discontinuidad:
\[y_i=\alpha+\tau D_i +\beta_0(x_i-x_0)+\beta_1(x_i-x_0)D_i+\varepsilon_i\]
Más aún, es posible combinar estas dos posibilidades para dar lugar a modelos más flexibles. Se espera que las conclusiones sean robustas al uso de modelos extremadamente complejos.
[5 puntos] ¿Qué factores podrían invalidar el uso de este método para evaluar el programa?
La principal preocupación es la posibilidad de manipulación del índice de riqueza para que la medición clasifique a los hogares como pobres. Podemos pensar en situaciones donde esto pudiera suceder con un individuo altamente sofisticado que pudiera manipular el reporte de forma estratégica para que su índice quedara por debajo del corte. Aunque difícil de suceder, esta posibilidad podría investigarse empíricamente, por ejemplo, verificando que no haya “amontonamientos” justo por encima de la discontinuidad.
Si existiera corrupción y muchos no elegibles recibieran la transferencia o si las familias no gastaran la transferencia en insumos que mejoren la función de producción de educación, el diseño también estaría comprometido.
Suponga que se propone ahora que la transferencia se realice a la cuenta del padre o la madre del estudiante. Se sabe que una de las consecuencias de esta decisión es que una fracción de los estudiantes no recibirá el dinero. Suponiendo que en una encuesta de seguimiento pudiera conocer si cada estudiante efectivamente recibió el pago, ¿cómo emplearía un diseño de regresión discontinua difusa para evaluar el efecto del programa sobre el desempeño escolar? En particular, describa:
[5 puntos] ¿Cómo estimaría la forma reducida? ¿Cuál es el coeficiente relevante y cuál es su interpretación?
El problema puede ser visto entonces como un diseño de regresión discontinua difusa. La discontinuidad define la probabilidad de recibir los fondos del programa. La forma reducida se estima con una regresión de la variable de desempeño escolar sobre el instrumento, que es estar por debajo del umbral. Al igual que cuando se estudió la interpretación del LATE, este coeficiente da la correlación entre el desempeño escolar y el estado del tratamiento, pero no toma en cuenta que el desempeño escolar también depende de la riqueza, una decisión endógena.
[5 puntos] ¿Cómo estimaría la primera y la segunda etapa? ¿Cuáles son los coeficientes relevantes y cuál es su interpretación?
La primera etapa consiste en estimar la relación entre la variable endógena y el instrumento. En este caso, el instrumento es una variable indicadora que toma valor de 1 si el índice de riqueza está por debajo del umbral. La decisión endógena es que los padres efectivamente entreguen la transferencia a los estudiantes. Se estima por una regresión de la variable endógena en función del instrumento.
La segunda etapa consiste en estimar el efecto de efectivamente recibir la transferencia sobre el desempeño escolar. Conceptualmente es como si se corriera una regresión de la variable de desempeño escolar en función de los valores ajustados en la primera etapa de la probabilidad de recibir la transferencia. En la práctica, nunca se estiman dos regresiones separadas, sino que se usa la definición del estimador de mínimos cuadrados en dos etapas. El coeficiente es el efecto de recibir la transferencia en el desempeño escolar.
[5 puntos] ¿Cuáles son los supuestos necesarios para estimar este modelo usando variables instrumentales?
Los supuestos econométricos para la estimación del modelo de regresión discontinua difusa son los mismos que para cualquier otro problema de variables instrumentales: 1) Exclusión: el instrumento no pertenece a la ecuación estructural; y 2) Relevancia de la primera etapa: el instrumento está correlacionado con la variable endógena.